３点を通る円の方程式の２通りの求め方と検算方法

解き方１：通る点を代入する方法

円の方程式の一般形は
$x^2+y^2+ax+by+c=0$
と書けるので、通る点を代入して $a,b,c$ を求めることができます。

$A(0,-3)$ を代入すると、
$0+9-3b+c=0$
つまり $3b-c=9$

$B(3,6)$ を代入すると、
$9+36+3a+6b+c=0$
つまり $3a+6b+c=-45$

$C(-1,-2)$ を代入すると、
$1+4-a-2b+c=0$
つまり $a+2b-c=5$

この三元一次連立方程式を解けばよいわけです。
$C$ の式を $-3$ 倍すると
$-3a-6b+3c=-15$
これと $B$ の式を足すと、
$4c=-60$
よって $c=-15$
これを $A$ の式に代入すると、
$3b+15=9$
よって $b=-2$
これを $C$ の式に代入すると、
$a-4+15=5$
よって $a=-6$

以上より、求める円の方程式は
$x^2+y^2-6x-2y+15=0$
となります。

解き方２：中心と半径を求める方法

中心が $(p,q)$ で半径が $r$ の円の方程式は、
$(x-p)^2+(y-q)^2=r^2$
と書けるので、中心と半径を求めればよいわけです。

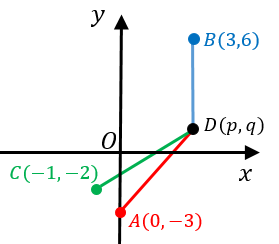
円の中心を $D(p,q)$ とおくと、
$DA$ の二乗は、
$p^2+(q+3)^2\\
=p^2+q^2+6q+9$
$DB$ の二乗は、
$(p-3)^2+(q-6)^2\\
=p^2-6p+9+q^2-12q+36$
$DC$ の二乗は、
$(p+1)^2+(q+2)^2\\
=p^2+2p+1+q^2+4q+4$

よって、$DA=DB$ なので、
$p^2+q^2+9+6q\\
=p^2+q^2+9-6p-12q+36$
$6q=-6p-12q+36$
$6p+18q=36$
① $p+3q=6$

また、$DA=DC$ なので、
$p^2+q^2+6q+9\\
=p^2+q^2+2p+4q+5$
$6q+9=2p+4q+5$
$2p-2q=4$
② $p-q=2$

①-②より、
$4q=4$
$q=1$、これと②より $p=3$
また、半径を $r$ とすると、
$r^2=DA^2\\
=3^2+4^2=25$

以上により、円の方程式は、
$(x-3)^2+(y-1)^2=25$

検算方法

検算方法１
外部サイトですが、検算用のツールを紹介します：
WolframAlpha

通る3点を打ち込んで Submit をクリックしてください。

検算方法２
求めた方程式にもとの点を代入して成立することを確認するという方法もあります。

次回は 円と直線の共有点の個数、座標、線分の長さ を解説します。