三角柱の表面積=底面積×2+側面積
例題
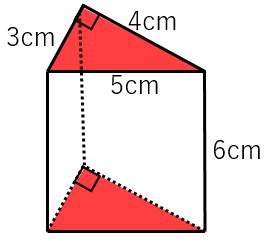
図のような三角柱の表面積を求めよ。

表面積は
底面積×2+側面積
です。
×2をしているのは、天井と底面の面積がともに「底面積」だからです。
この問題では、底面は直角三角形なので、
底面積は、$3\times 4\div 2=6\:\mathrm{cm}^2$
です。
側面は長方形3枚なので、面積をそれぞれ計算すると、
$5\times 6=30\:\mathrm{cm}^2$
$3\times 6=18\:\mathrm{cm}^2$
$4\times 6=24\:\mathrm{cm}^2$
よって、側面積は
$30+18+24=72\:\mathrm{cm}^2$
です。
よって、表面積は、
$6\times 2+72=84\:\mathrm{cm}^2$
となります。
計算ツール
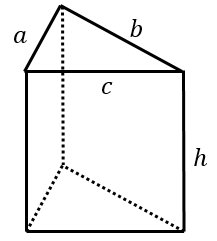
一般的な公式
各辺の長さを $a,b,c,h$ としてみましょう。
側面積は長方形3枚の面積の足し算なので、
$ah+bh+ch=(a+b+c)h$
で計算できます。

底面積は、計算が大変です。
(さきほどの例題は底面が直角三角形だったので簡単に面積が分かりましたが、いつもそううまくいくとは限りません)
ヘロンの公式(高校数学で習う公式です)というものを使うと、底面積は、
$S=\sqrt{s(s-a)(s-b)(s-c)}$
(ただし、$s=(a+b+c)\div 2$)
となります。
よって、表面積は、
$2\sqrt{s(s-a)(s-b)(s-c)}+2sh$
となります。
例えば、さきほどの例題の場合、$a=3$、$b=4$、$c=5$、$h=6$ として、
$s=\dfrac{3+4+5}{2}=6$
なので、表面積は
$2\sqrt{6\times 3\times 2\times 1}+2\times 6\times 6\\
=12+72\\
=84\:\mathrm{cm}^2$
となります。
次回は 円柱の表面積と体積を求める公式 を解説します。
