確率変数 $X$ に対して、
$F(x)=P(X\leq x)$
($X$ の値が $x$ 以下になる確率)
のことを累積分布関数と言う。
累積分布の例
$X$ とします。
このとき、
表が0回出る確率は $\dfrac{1}{8}$
表が1回出る確率は $\dfrac{3}{8}$
表が2回出る確率は $\dfrac{3}{8}$
表が3回出る確率は $\dfrac{1}{8}$
と計算できます。
この結果をふまえると、
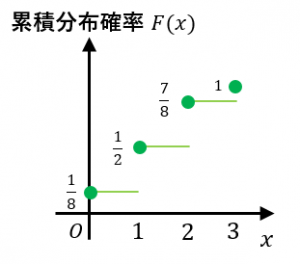
表が0回以下の確率は $\dfrac{1}{8}$
表が1回以下の確率は $\dfrac{1}{8}+\dfrac{3}{8}=\dfrac{1}{2}$
表が2回以下の確率は $\dfrac{1}{8}+\dfrac{3}{8}+\dfrac{3}{8}=\dfrac{7}{8}$
表が3回以下の確率は $1$
です。この状況を表現するのが累積分布関数 $F(x)$ です。
確率密度関数との関係
$F(x)=P(X\leq x)$
(値が $x$ 以下になる確率)
のことを累積分布関数と言います。
$F(a)$ は、値が $a$ 以下になる確率を表すので、確率密度関数 $p(x)$ の $[-\infty,a]$ 部分の面積になります。
つまり、
$F(a)=\displaystyle\int_{-\infty}^ap(x)dx$
が成立します。

例題
平均 $\dfrac{1}{\lambda}$ の指数分布の確率密度関数は、$p(x)=\lambda e^{-\lambda x}\:(x\geq 0)$ で与えられる。この分布の累積分布関数を求めよ。
解答:
$F(a)=\displaystyle\int_0^a\lambda e^{-\lambda x}dx\\
=[-e^{-\lambda x}]_0^a\\
=1-e^{-\lambda a}$
となります。
累積分布の性質
・累積分布関数は、単調非減少です。
・累積分布関数は、右連続です(右側から近づいていったときにジャンプしないというイメージです)。左連続とは限りません。
・$\displaystyle\lim_{x\to -\infty}F(x)=0$、$\displaystyle\lim_{x\to\infty}F(x)=1$
次回は キュムラントとキュムラント母関数 を解説します。
