立方体と直方体の表面積を計算する

立方体と直方体の表面積を計算する公式を解説し、例題を解いてみます。

立方体の表面積

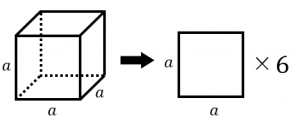
一辺の長さが $a$ の正方形の面積は $a^2$ です。
立方体は正方形 $6$ 枚からできているので、
一辺の長さが $a$ の立方体の表面積は、
$a^2\times 6=6a^2$
となります。

解答：
一辺の長さが $2\:\mathrm{cm}$ の正方形の面積は、
$2\times 2=4\:\mathrm{cm}^2$
です。
よって、立方体の表面積は、
$4\times 6=24\:\mathrm{cm}^2$
となります。

計算ツール

直方体の表面積

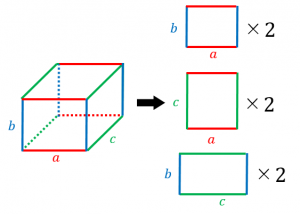
この直方体は、図のように、3つのタイプの長方形を2枚ずつ集めてできたものです。
そのため、表面積は、
$a\times b\times 2 + b\times c\times 2+c\times a\times 2$
$=2(ab+bc+ca)$
となります。

解答：
公式を使うと、
$2(3\times 4+4\times 5+5\times 3)=94\:\mathrm{cm}^2$
となります。

計算ツール

次回は 立方体と直方体の体積を計算する方法とツール を解説します。