ねじれの位置の意味と直方体、三角柱、五角柱での例

ねじれの位置の意味と、代表的な具体例を分かりやすく説明します。
例題を通して、空間図形における「ねじれの位置」を確実に理解しましょう。

ねじれの位置とは

空間にある２本の直線が次の２条件をともに満たすとき、
２本の直線はねじれの位置にあると言います。

・交わらない
・平行でない

直方体の例

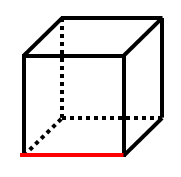
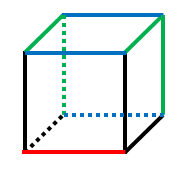
・黒い辺は４本ありますが、いずれも 赤い辺 と隣接しており、交わるためねじれの位置ではありません。
・青い辺 は３本あり、いずれも 赤い辺 と平行なので、ねじれの位置ではありません。
・緑の辺 は４本あり、赤い辺 と交わりもせず、平行でもありません。したがって、ねじれの位置にあります。

よって、赤い辺とねじれの位置にある辺は４本です。

このように、ねじれの位置を調べるときは

1. 交わるもの（隣接する辺）
2. 平行なもの
3. 残ったもの

の順に分類すると判断しやすくなります。

三角柱の例

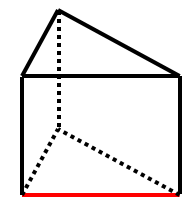
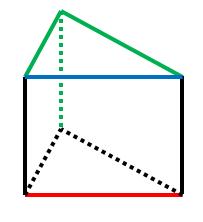
・黒い辺は 赤い辺 と隣接し交わるため、ねじれの位置ではありません。
・青い辺 は 赤い辺 と平行です。
・緑の辺 は 赤い辺 と交わらず、平行でもないため、ねじれの位置にあります。

よって、赤い辺とねじれの位置にある辺は３本です。

五角柱の例

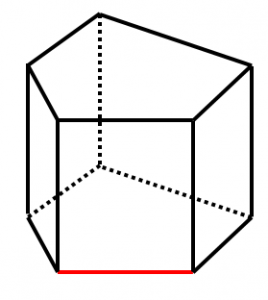
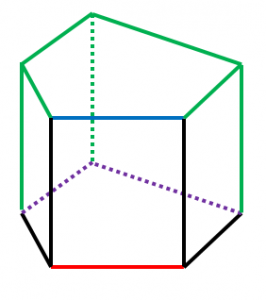
・黒い辺は 赤い辺 と隣接し交わるため、ねじれの位置ではありません。
・紫の辺 は隣接こそしていませんが、底面という同一平面上にあり、延長すれば交わるため、ねじれの位置ではありません。
・青い辺 は 赤い辺 と平行です。
・緑の辺 は交わらず、平行でもないため、ねじれの位置にあります。

よって、赤い辺とねじれの位置にある辺は７本です。

補足

紫の辺 がねじれの位置に「ならない」点が重要です。
辺同士のねじれを考えるときの「交わらない」は、「延長しても交わらない」という意味で判断します。

ねじれの位置の定義の言い換え

ねじれの位置の定義に出てくる
「交わらない」かつ「平行でない」
という条件は、次のように言い換えられます。

同じ平面上にない

すなわち、

「空間にある２本の直線が、同一平面上にないとき、それらはねじれの位置にある」

という言い換えも成立します。

次回は 正多面体の辺の数と頂点の数の求め方 を解説します。