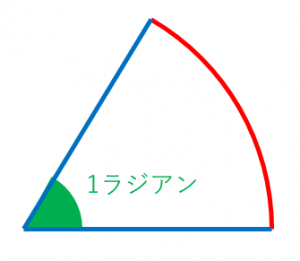
ラジアンは「度」と同じく、角度の大きさを表す単位です。弧の長さと半径が等しくなるようなおうぎ形の中心角が1ラジアンです。1ラジアンはおよそ57°です。ラジアンのことを rad と書くことがあります。
このページでは、ラジアン(rad)という角度について、意味や度数(°)に変換する方法を解説します。
ラジアンとは
1ラジアンの定義は?
弧の長さと半径が等しくなるようなおうぎ形の中心角を1ラジアンと定めます。

同様に、弧の長さが半径の2倍になるようなおうぎ形の中心角は2ラジアンです。
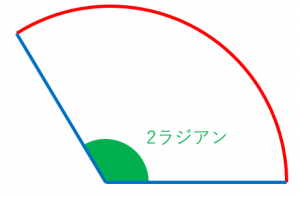
同様に、弧の長さが半径の $X$ 倍になるようなおうぎ形の中心角が $X$ ラジアンです。
1ラジアンはどれくらいの大きさ?
1ラジアンは、$\dfrac{180}{\pi}$ 度です。つまり、およそ57.3°です。理由は後で述べます。
ラジアンを度に変換する
$1$ ラジアン=$\dfrac{180}{\pi}$度
という式を使います。
$\dfrac{180}{\pi}$ はおよそ $57.3$ です。
例えば、2ラジアンは、
$2\times 57.3=114.6$ なので、およそ $115$° になります。
また、Google 検索窓で「2ラジアン 度」のように入力すると、ラジアンを度に変換してくれます。
| ラジアン | $0$ | $1$ | $2$ | $3$ | $\pi$ |
| 度 | $0$ | 約$57^{\circ}$ | 約 $115^{\circ}$ | 約 $172^{\circ}$ | $180^{\circ}$ |
度をラジアンに変換する
$1^{\circ}=\dfrac{\pi}{180}$ ラジアン
という式を使います。
度をラジアンに変換するときは、$\dfrac{\pi}{180}$ をかけます。
例えば、$60^{\circ}$ をラジアンに直すと、
$60\times\dfrac{\pi}{180}=\dfrac{\pi}{3}$
つまり $\dfrac{\pi}{3}$ ラジアンになります。
| 度 | $0^{\circ}$ | $30^{\circ}$ | $45^{\circ}$ | $60^{\circ}$ | $90^{\circ}$ |
| ラジアン | $0$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ |
| 度 | $120^{\circ}$ | $135^{\circ}$ | $150^{\circ}$ | $180^{\circ}$ |
| ラジアン | $\dfrac{2}{3}\pi$ | $\dfrac{3}{4}\pi$ | $\dfrac{5}{6}\pi$ | $\pi$ |
※表では弧度法の単位「ラジアン」は省略しています。
という関係式が重要です。
ラジアンと度の変換式の証明
弧の長さが半径の $X$ 倍になるようなおうぎ形の中心角が $X$ ラジアンでした。
そこで「中心角が180度のおうぎ形」を考えてみます。このおうぎ形では、
弧の長さ=$\pi\times$ 半径
という式が成立します。
つまり、このおうぎ形の中心角は $X=\pi$ ラジアンになります。つまり、$180^{\circ}$ と $\pi$ ラジアンは同じ大きさの角度を表すことが分かりました。
また、
$180^{\circ}=\pi$ ラジアン
の両辺を $180$ で割ると、
$1^{\circ}=\dfrac{\pi}{180}$ ラジアン
であることも分かります。
次回は 弧の長さと弦の長さの求め方、円周角との関係など を解説します。
