ランダムフォレスト(Random Forest)とは、
・分類や回帰に使える機械学習の手法
・決定木をたくさん作って多数決する(または平均を取る)ような手法
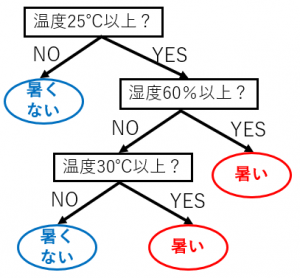
そもそも決定木とは
決定木とは、分類(や回帰)のルールをツリーで表現したものです。
ランダムフォレストで何ができるか?
例えば、図のように分類木をたくさん集めたもので多数決を取ると、全体として1つの分類器になります。
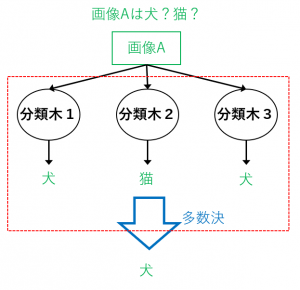
単純に1つの分類木のみで分類するよりも、精度が高くなりやすいです(1人で決めるよりも、大人数で相談して決めた方が間違えにくい、というイメージ)。
また、回帰問題に対しては、回帰木をたくさん集めたランダムフォレストを使うことができます。この場合、全体の代表値(例えば平均値)を予測値として出力とします。
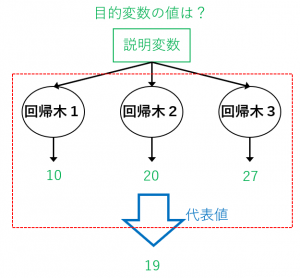
どのように決定木を作成するか
ランダムフォレストにおける学習では、たくさんの決定木を作りますが、それぞれの決定木が似たようなものだと多数決を取る意味があまりありません(偏った人だけでなく、いろいろな考え方の人で多数決を取った方が全体の精度が高くなりそう、というイメージ)。
そこで、各決定木を、
1.それぞれ異なるデータをもとにする
2.異なる説明変数を分割の候補として使う
という方針で作成し、木の多様性を確保します。
この1、2がポイントで、それぞれランダム性が登場します。
1.それぞれ異なるデータをもとにする
ランダムフォレストでは、もとの訓練データから、(各 $i$ に対して)$i$ 番目の決定木を作成するための「サブ訓練データ」を抽出します。それぞれの抽出は復元抽出で行います(同じデータを何回も抽出することもある)。このように、復元抽出によってサブデータを作成する手法を、ブートストラップサンプリングと言います。
例えば、もとのデータが $(d_1,d_2,d_3,d_4,d_5)$ の5つからなるとき、
・1番目の決定木の作成には $(d_1,d_2,d_4,d_4)$ を使い
・2番目の決定木の作成には $(d_1,d_3,d_4,d_5)$ を使う
というような感じです。
2.異なる説明変数を分割候補として使う
各決定木を作成するときには、1つのノードから初めてどんどん分割していくわけですが、分割は、
訓練データの説明変数のうち、$K$ 個をランダムに選び、その $K$ 個の中で最もうまく分割できるような変数で分割する
という方針で行います。全ての変数ではなく、(分割のたびに異なる)ランダムに選んだ $K$ 個の説明変数の中から分割する変数を選ぶというのがポイントです。
※「うまく」というのは「ジニ不純度」など何らかの基準で判断します。
※ $K$ は最初に決めておくパラメータです。
ランダムフォレストの利点
・決定木をもとにした手法なので、出力結果の説明が比較的しやすいです。(DNN などは出力結果を説明しにくい)
・各決定木を作成する計算は並列化できるので、高速な計算が可能です。
次回は ブースティングとアダブースト(AdaBoost)について詳しく解説 を解説します。
