施策の効果を測る「傾向スコアマッチング」や「逆確率重み付け法」について、大雑把に分かりやすく解説します。因果推論という分野の基本的な手法です。
施策の効果は「平均の差」で測れる?
・全部で30人会員がいるジム
・15人にクーポンを配った
という状況を考えます。
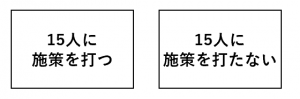
このときクーポンという施策の効果は、例えば、翌月の
「施策を打った15人の平均売上額」ー「施策を打たなかった15人の平均売上額」
で計算できそうです。
実際、クーポンを打つ15人がランダムに選ばれていれば、基本的には上の計算式で施策の効果(ATE、Average Treatment Effect)を測ることができます。ABテスト、RCT(Randomized Controlled Trial)などと言います。
「平均の差」ではうまくいかない場合
・クーポンは男性に多めに打った
・そもそも売上額は男性の方が多い
としましょう。
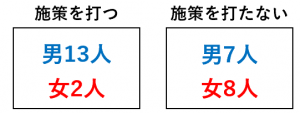
この場合、男性と女性では状況が違うので、施策の効果を単純に
「施策を打った15人の平均売上額」ー「施策を打たなかった15人の平均売上額」
で計算してはいけません。
売上額が多い男性が多く含まれている「施策を打った15人の平均売上額」が高くなるのは当然なので、クーポンに効果が無かったとしても、上記の「平均の差」はプラスになるでしょう。
交絡因子とは
上の状況で、
「性別」は「施策を打つか打たないか」に影響を与えます。
「性別」は「目的変数」(この場合売上額)に影響を与えます。
このように「目的変数」と「施策を打つか打たないか」の両方に与える説明変数を交絡因子と言います。
上の例で「性別」は交絡因子です。交絡因子があるときには、単純に「施策を打った群の平均」ー「施策を打たなかった群の平均」で施策の効果を計算してはいけません。
傾向スコアマッチング
傾向スコアマッチングでは、交絡因子の影響が等しくなるように、それぞれの群で代表者に限定して平均を比較します。
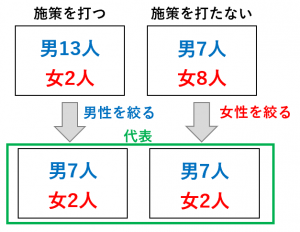
例えば、先ほどの状況では、それぞれの群から男性7人女性2人を抽出して
「施策を打った群の代表9人の平均」ー「施策を打たなかった群の代表9人の平均」
で施策の効果を計算します。
両群で男性、女性の人数が等しいので、性別の影響を排除できています。ただし、使ったデータ数が少なくなります。
傾向スコアとは

例の場合、女性10人のうち2人に施策を打っているので、
女性の傾向スコアは $0.2$
と言えます。
同様に、男性の傾向スコアは$13\div 20=0.65$ になります。
傾向スコアマッチングは「傾向スコアが等しいものどうしを代表者として抽出して」平均を比較する手法と言えます。
逆確率重み付け法

この例では、以下のように施策の効果を計算することもできそうです!
男性における施策の効果:
「施策を打った男性 $13$ 人の平均」ー「施策を打たなかった男性 $7$ 人の平均」
女性における施策の効果:
「施策を打った女性 $2$ 人の平均」ー「施策を打たなかった女性 $8$ 人の平均」
をそれぞれ計算して、最後にそれぞれの人数で重み付き平均を取る:
全体の効果=$\dfrac{20}{30}\times$男性における施策の効果$+\dfrac{10}{30}\times$女性における施策の効果
この式の右辺は、少し変形すると、
$\dfrac{1}{30}\displaystyle\left(\sum_{i\in A}\dfrac{y(i)}{e(i)}-\sum_{i\in B}\dfrac{y(i)}{e(i)}\right)$
となることが確認できます。ただし、$A$ は施策を打った人の集合、$B$ は施策を打たなかった人の集合、$y(i)$ は $i$ の施策効果、$e(i)$ は $i$ の傾向スコアです。
つまり、傾向スコアの逆数で重みを付けて、施策効果の平均の差を見たと言えます。上式で施策の効果を計算する手法を逆確率重み付け法(Inverse Propensity Weighting、IPW)と言います。
次回は マルコフ連鎖の定常分布と極限分布 を解説します。
