パレート分布の意味、期待値、分散

パレート分布の性質

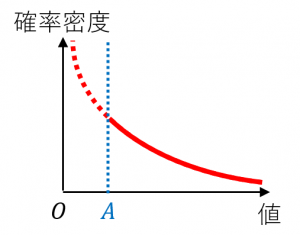
・確率変数のとりうる値の範囲は、$x\geq A$ です。
・$x$ の増加につれて、密度関数の値は減少していきます。
・ただし、減少の勢いは、正規分布よりも緩やかです。指数関数的な減少ではなく、べき関数に依って減少していくので「べき分布」と呼ばれることがあります。なかなか減少していかないので、裾が重い分布と呼ばれることもあります。
・パレート分布の中では、$k$ がより大きい分布の方が、減少が急激です。

正規化定数について

$k$ が $1$ より大きいとき、
$\displaystyle\int_A^{\infty}\dfrac{1}{x^k}dx\\
=\dfrac{A^{1-k}}{k-1}\\
=\dfrac{1}{(k-1)A^{k-1}}$
です。

よって、$C=(k-1)A^{k-1}$ となります。つまり、密度関数は、
$f(x)=\dfrac{(k-1)A^{k-1}}{x^k}$
となります。

$k-1$ を $K$ と置き直すと、密度関数は、
$f(x)=\dfrac{KA^K}{x^{K+1}}$
と表すこともできます。

期待値

期待値の定義に従って計算を試みると、
$\displaystyle\int_A^{\infty}xf(x)dx\\
=C\displaystyle\int_A^{\infty}\dfrac{1}{x^{k-1}}dx\\$
となります。この定積分の部分は、$k > 2$ のときに収束し、その値は、
$\dfrac{A^{2-k}}{k-2}$
となります。よって、これに $C=(k-1)A^{k-1}$ をかけると、
$\dfrac{k-1}{k-2}A$
となります。

分散

$\mathrm{Var}[X]=E[X^2]-E[X]^2$
であり、$k> 3$ のとき二次モーメントは、
$E[X^2]=\displaystyle\int_A^{\infty}\dfrac{C}{x^{k-2}}dx\\
=(k-1)A^{k-1}\dfrac{A^{3-k}}{k-3}\\
=\dfrac{(k-1)A^2}{k-3}$
となります。

よって、期待値の計算結果と合わせると、
$\mathrm{Var}[X]\\
=\dfrac{(k-1)A^2}{k-3}-\dfrac{(k-1)^2}{(k-2)^2}A^2\\
=\dfrac{(k-1)}{(k-2)^2(k-3)}A^2$
となります。

次回は 逆ガンマ分布 を解説します。