ナップサック問題の問題設定と、動的計画法(表を順々に埋めていく方法)による解き方を解説します。
ナップサック問題とは
・荷物が $N$ 個ある
・各 $i$ に対して、$i$ 番目の荷物は重さが $w_i$、価値が $v_i$
・ナップサックには合計重さ $W$ までしか荷物が入らない
・荷物をナップサックにうまく入れて、価値を最大化したい
というのがナップサック問題です。
※各荷物は「入れるか入れないかの2通り」とします。この問題設定を0-1 ナップサック問題と言います。
ナップサック問題は難しい
単純に考えると、入れる荷物の選び方を全て考えれば解けますが、荷物の選び方は全部で $2^N$ 通りあるので、総当りで解くのは厳しいです。
実際、ナップサック問題はNP困難と呼ばれる(計算量理論において)難しい問題のクラスに属していることが知られています。
動的計画法で解く(方針)
$1$ 番目から $i$ 番目までの荷物のみを使って、容量 $w$ のナップサックに詰め込める価値の最大値を $V(i,w)$ とします。最終的に求めたいのは $V(N,W)$ です。
今回紹介する動的計画法の方針としては $i$ と $w$ が小さいところから順々に $V(i,w)$ を求めていく方法です。上から順に、左から順に $V(i,w)$ の値が格納された表を埋めていくイメージです。
動的計画法で解く(表の埋め方)
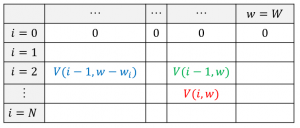
まず、1行目($i=0$ の行)は全て $0$ が入ります。(荷物 $0$ 個では何も詰められないと考えます)
次に、2行目以降についてですが、$i$ 行目は $(i-1)$ 行目の結果から計算することができます。具体的には、
$V(i,w)=\max\{V(i-1,w),V(i-1,w-w_i)+v_i\}$
という漸化式を使って計算することができます。
$V(i,w)$ は「$1$ 番目から $i$ 番目までの荷物のみを使って、容量 $w$ のナップサックに詰め込める価値の最大値」でした。これを以下の2通りに場合分けして求めます。
・$i$ 番目の荷物を使わない場合
この場合の値は「$1$ 番目から $(i-1)$ 番目までの荷物のみを使って、容量 $w$ のナップサックに詰め込める価値の最大値」と等しいので、$V(i-1,w)$ です。
・$i$ 番目の荷物を使う場合
この場合の価値の最大値は「$1$ 番目から $(i-1)$ 番目までの荷物のみを使って、容量 $(w-w_i)$ のナップサックに詰め込める価値の最大値、に $i$ 番目の荷物の価値を加えたもの」と等しいので、$V(i-1,w-w_i)+v_i$ です。
※ただし、$w_i$ が $w$ より大きい場合は、$i$ 番目の荷物はそもそも使えません。つまり、$w_i > w$ の場合は、こちらの場合分けを無視する、または $V(i-1,w-w_i)=-\infty$ と考えてください。
上記の2つの値の大きい方が $V(i,w)$ になるので、漸化式が証明できました。
上の漸化式を使えば、上のマスと左上の方のマスが埋まっていれば、それをもとに新たなマスを埋めることができます。
このようにして順々にマスを埋めていけば、最終的に求めたい $V(N,W)$ が分かります。また、$V(N,W)$ を埋める過程で使われたルートをたどっていくと、$V(N,W)$ を達成する荷物の入れ方も分かります(詳細は省略します)。
次回は 編集距離(レーベンシュタイン距離)の求め方 を解説します。
