編集距離（レーベンシュタイン距離）の求め方

編集距離とは

「すうがく」という単語を最低何回「編集」すれば「すがた」という単語になるでしょうか？

ただし「編集」とは、
一文字挿入、一文字削除、一文字置換
のいずれかの操作のこととしましょう。

例えば、
「すうがく」の「う」を削除
→「すがく」の「く」を「た」に置換
→「すがた」
となり、「すうがく」から「すがた」へは編集２回で行けることになります。（編集１回では行けません）

このように、必要な「編集」の最低回数のことを編集距離と言います。
つまり「すうがく」と「すがた」の編集距離は $2$ です。

レーベンシュタイン距離

「編集」で許す操作は、挿入または削除または置換としましたが、置換を許さないなど、他にもバリエーションがあります。

このように「編集」の定義はいろいろありますが、挿入または削除または置換という「編集」による編集距離を、特にレーベンシュタイン距離と言います。
参考：Levenshtein distance

レーベンシュタイン距離の求め方

レーベンシュタイン距離は、動的計画法という手法を用いて求めることができます。具体的なアルゴリズムを、「すうがく」と「すがた」の例で説明します。

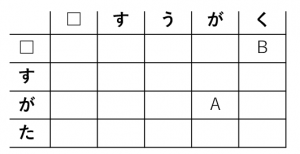
・２つの単語を、それぞれ縦と横に並べます。
・一行目、一列目は空文字に対応します。
・各マスに、対応する２つの部分文字列のレーベンシュタイン距離を入れていくのが目標です。例えば、Aには「すうが」と「すが」のレーベンシュタイン距離が入り、Bには、「すうがく」と空文字のレーベンシュタイン距離が入ります。

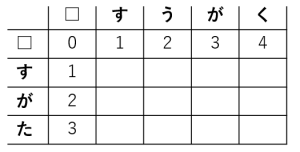
・空文字と「$n$ 文字の文字列」のレーベンシュタイン距離は $n$ なので、一行目と一列目が埋まります。

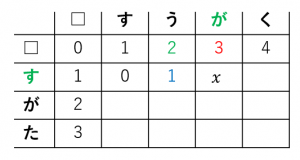
各マスには、以下の３つの中で一番小さい数字を入れます。
・自分のマスの上のマスの数字 $+1$
・自分のマスの左のマスの数字 $+1$
・自分のマスの左上のマスの数字 $+c$
（ただし自分の縦と横の文字が等しい場合は $c=0$、異なる場合は $c=1$）

例えば、$x$ のマスは、
・上が $3$
・左が $1$
・左上が $2$（「が」と「す」は異なるので $c=1$）
なので、$1+1=2$ が入ります。

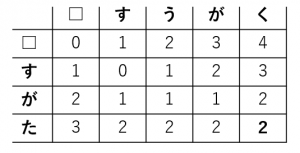
「すうがく」と「すがた」のレーベンシュタイン距離は２です。

アルゴリズムがなぜ正しいか

$a_1\dots a_N$ という文字列を $b_1\dots b_M$ に最短の編集回数で編集するにはどうすればよいでしょうか？
以下の３つの方法が考えられます。（※）
方法１：$a_1\dots a_N$ という文字列を $b_1\dots b_{M-1}$ に編集してから $b_M$ を挿入
方法２：$a_1\dots a_{N-1}$ の部分を $b_1\dots b_M$ に編集してから末尾の $a_N$ を削除
方法３：$a_1\dots a_{N-1}$ の部分を $b_1\dots b_{M-1}$ に編集してから末尾の $a_N$ を $b_M$ に置換。（$a_N=b_M$ なら置換は不要）
それぞれが、手順３の各値に対応しています。

※厳密には、上記の３つの方法のいずれかで、必ず最短が実現できることを説明する必要があります。これは、真の最短手順において、$b_M$ がどこに由来するかで場合分けすれば確認できます。
・$b_M$ が新たに登場した場合、方法１で実現できます。
・$a_1$ から $a_{N-1}$ のいずれかが $b_M$ になった場合、方法２で実現できます。
・$a_N$ が $b_M$ になった場合、方法３で実現できます。

次回は TF-IDF（単語の重要度の評価指標） を解説します。