強化学習で登場するマルコフ決定過程(Markov Decision Process)というモデルについて、大雑把に説明します。
迷路の例
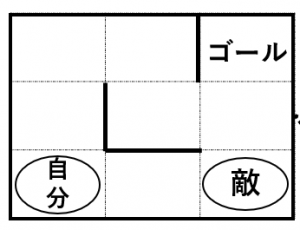
自分が1マス好きな向きに動く
→敵が1マスランダムに動く
ことを繰り返して、敵に重ならないようにゴールを目指すゲームを考えることにします。
マルコフ決定過程とは
$S$:状態の集合
$A$:行動の集合
$P$:遷移確率
$R$:報酬
迷路の例では、以下のようになります。
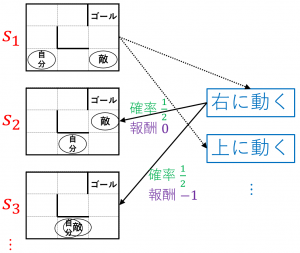
状態の集合 $S=\{s_1,s_2,\dots\}$
「自分が一番左下のマスにいて敵が右下にいる状態」など、全てのとりうる状態を集めたものが $S$ です。
行動の集合 $A=\{a_1,a_2,\dots\}$
「自分が右に動く」「自分が上に動く」など、自分がとれる行動を集めたものが $A$ です。
遷移確率 $P(s,a,s’)$
状態 $s$ において行動 $a$ をとったときに、次の状態が $s’$ になる確率 $P(s,a,s’)$ も与えられています。例えば、図の $s_1$ の状態で「$a_1=$ 右に動く」という行動をとったとき、敵は上か左にそれぞれ確率 $\dfrac{1}{2}$ で動くので、$P(s_1,a_1,s_2)=P(s_1,a_1,s_3)=\dfrac{1}{2}$ となります。
報酬 $R(s,a,s’)$
「状態 $s$ において行動 $a$ をとって、次の状態が $s’$ になった」ときにどれくらい嬉しいかを表す量 $R(s,a,s’)$ も与えられています。「嬉しさ」は直前の状態 $s$ や行動 $a$ には依存せず、結果の状態 $s’$ のみに依存することも多いので、$R(s’)$ と書くこともあります。迷路の例だと、例えば、$s’$ でゴールにたどりついていれば $R(s’)=1$ 、敵と自分の位置が一致していたら $R(s’)=-1$、それ以外は $R(s’)=0$ とします。
マルコフ決定過程でやりたいこと
「もらえる報酬が最大になりそうな」のきちんとした定式化は、強化学習の文献などを参照してください。
「行動方針」の意味は説明します。
行動方針とは
強化学習の文脈では政策(Policy)と呼ばれることが多いです。
例えば、状態 $s_1$ にいるときは行動 $a_1$ をとり、$s_2$ にいるときには行動 $a_3$ をとる、というような規則です。
また、確率的な政策を考えることも多いです。例えば、状態 $s_1$ にいるときは確率 $0.9$ で行動 $a_1$ をとり、確率 $0.1$ で行動 $a_2$ をとる、というような規則です。
次回は 隠れマルコフモデルの大雑把な解説 を解説します。
