隠れマルコフモデルの大雑把な解説

隠れマルコフモデル（Hidden Markov Model, HMM）について、大雑把に解説します。

隠れマルコフモデルとは

例えば、状態として「元気」または「風邪」の２値を考えます。そして、
１．今日の状態は昨日の状態のみに依存する
２．「風邪」か「元気」かは分からない
３．「風邪」の場合は確率0.8で熱が37度以上。「元気」の場合は確率0.1で熱が37度以上
とします。

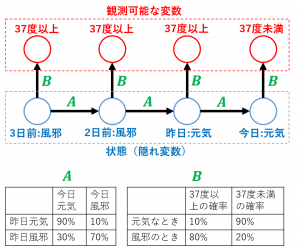
隠れマルコフモデルの主なパラメータは、
・$A$：状態遷移確率
・$B$：状態と観測可能変数の関係（を表す確率分布）
です。

隠れマルコフモデルでやりたいこと１

上の例だと、
$A$ と $B$ と、熱が37度以上かどうかという情報から、各日で「元気」だったのか「風邪」だったのかを推定します（元気か風邪かという状態は、直接は分からないが、熱があるかという情報から推定しよう）。

ビタビアルゴリズムというアルゴリズムを使うことで実現できます。

隠れマルコフモデルでやりたいこと２

上の例だと、
熱が37度以上かどうかという情報から、$A$ と
$B$ の各マスの数字を推定します。

バウム・ウェルチアルゴリズムというアルゴリズムを使うことで実現できます。

諸注意

・ある時点の状態は１つ前の状態にのみ依存する、というのは一次のマルコフモデルの話です。二次以上のマルコフモデルを考えることもできます。

・厳密には、
「状態遷移確率」
「状態と観測可能変数の関係（を表す確率分布）」
に加えて
「初期状態分布（時刻 $t=1$ で各状態にある確率）」
も隠れマルコフモデルのパラメータです。

・本ページは「大雑把な理解」を目的としたものです。数式を用いた厳密な説明は、専門書を参照してください。

次回は 状態空間モデルの意味と4つの分類（線形性、正規性、時変性、連続性） を解説します。