ハフ変換(Hough変換)とは、画像や点の集合の中から、直線や円など特定のパターンを検出する手法です。
問題設定
例えば、図のような点の集合を考えます。画像に対して特徴的な点のみを描画したものと考えてもよいです。
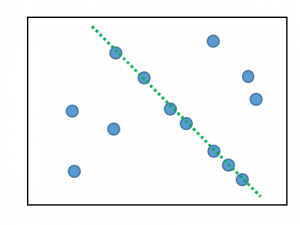
このような点の集合から、直線や円など特定のパターンを検出する問題を考えます。
例えば「直線を検出する」という問題に対して、人間の目では、緑の点線あたりが答えだと認識できますが、これをプログラムで行うのが目的です。
ハフ変換による直線検出の手順
手順1. 各点 $(x_0,y_0)$ に対して、$(r,\theta)$ 平面に $r=x_0\cos\theta+y_0\sin\theta$ という曲線を描画する:
例えば、点の集合に $(1,0)$ が含まれる場合 $r=\cos\theta$ という曲線を描画します。
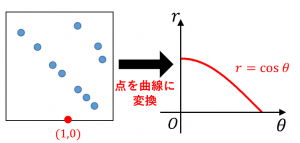
$(r,\theta)$ 平面には、もとの画像における点の数だけ曲線が描画されることになります。
手順2. $(r,\theta)$ 平面で、たくさんの曲線が交わった点を求める:
手順1で描画した曲線の多くが、偶然特定の点 $(r^*,\theta^*)$ を通ったとしましょう。
これは、もとの画像において、$r^*=x_0\cos\theta^*+y_0\sin\theta^*$ を満たすような $(x_0,y_0)$ がたくさんあることを意味します。
言い換えると、$r^*=x\cos\theta^*+y\sin\theta^*$ という直線に多くの点が乗っていることを表します。めでたく、多くの点が乗っているような直線が検出できました。
ハフ変換の意味(手順1の補足)
もう少し詳しく解説します。
$r=x\cos\theta+y\sin\theta$ は、$(r,\theta)$ を固定すると、$xy$ 平面における直線を表します。そして、この直線が $(x_0,y_0)$ を通るとき、$r$ と $\theta$ の間には $r=x_0\cos\theta+y_0\sin\theta$ という関係が成立します。
つまり「$(x_0,y_0)$ を通る直線全体の集合」は「$r=x_0\cos\theta+y_0\sin\theta$ を満たす $(r,\theta)$ の集合」に対応します。
よって、
複数の点に対応する曲線 $r=x_0\cos\theta+y_0\sin\theta$ が $(r,\theta)$ 平面で交わる
⇔複数の点について、各々を通る直線の集合に共通の要素がある
⇔複数の点は、実は同一直線上にある
と言えます。
このように、$(x_0,y_0)$ という点を「$(x_0,y_0)$ を通る直線全体の集合」に対応させる操作のことをハフ変換と言います。
手順2の補足
手順2で、多くの曲線が厳密に同じ点で交わることはほぼありません。実際には「たくさんの曲線が交わった点を求める」のではなく「たくさんの曲線が近くを通る点を求める」という計算を行います。
ハフ変換の一般化
直線検出では、$(x_0,y_0)$ に対して「$(x_0,y_0)$ を通る直線全体の集合」を対応させるようなハフ変換を考えました。
これを一般化すると、他の特定のパターンの検出にも使えます。例えば、円検出では、$(x_0,y_0)$ に対して「$(x_0,y_0)$ を通る円全体の集合」を対応させるようなハフ変換を考えます。
「$(x_0,y_0)$ を通る円全体の集合」は、$(x_0-A)^2+(y_0-B)^2=R^2$ を満たす $(A,B,R)$ の集合に対応します。
直線検出の場合には、ハフ変換の行き先は $(r,\theta)$ という二次元平面でしたが、円検出の場合には、$(A,B,R)$ という三次元空間になります。
また、螺旋を検出するのにハフ変換が使えたりもします。(例. Kaggle の CERN コンペ)
次回は 無作為抽出(ランダムサンプリング)の意味と実施する方法 を解説します。
