LASSO回帰とRidge回帰の意味を解説します。
また、それぞれのメリット:
・LASSO回帰の解はスパースになりやすいので嬉しい。
・Ridge回帰の解は解析的に書けるので嬉しい。
についても解説します。
LASSO回帰、Ridge回帰とは
普通の最小二乗法:
「予測と実際の値の二乗誤差」を最小化
$\displaystyle\min_w\sum(y-f(w,x))^2$
LASSO回帰:
「予測と実際の値の二乗誤差」を小さくしつつ「モデルが複雑になりすぎないように $w$ の大きさ(L1ノルム)も小さくする」
$\displaystyle\min_w\sum(y-f(w,x))^2+$$\lambda\|w\|_1$
ただし,1ノルムとは、各成分の絶対値の和:
$\|w\|_1=|w_1|+\dots +|w_n|$
Ridge回帰:
「予測と実際の値の二乗誤差」を小さくしつつ「モデルが複雑になりすぎないように $w$ の大きさ(L2ノルム)も小さくする」
$\displaystyle\min_w\sum(y-f(w,x))^2+$$\lambda\|w\|^2_2$
ただし,L2ノルムとは、各成分の二乗和のルート:
$\|w\|_2=\sqrt{w_1^2+\dots +w_n^2}$
LASSOの特徴
- ・LASSO回帰のことをL1正則化とも言う。
- ・LASSOはleast absolute shrinkage and selection operatorの略なので、全て大文字。
- ・LASSOの解はスパースになりやすい(0成分が多くなりがち)ので嬉しい。
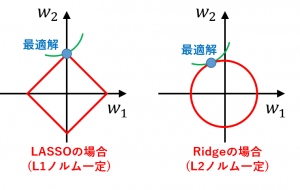
実際L1ノルムが一定である線はとがっているので、最適解が座標軸上になりやすいです。
補足:
最適解において二乗誤差が一定である線とL1ノルムが一定である線は接します。(そうでない場合、2つの線がクロスするとどちらかに移動することで目的関数値をさらに小さくできてしまう)
そして、L2ノルムの場合は(L1ノルムの場合と比較して)接点が座標軸上になりにくいです。
Ridgeの特徴
- ・Ridge回帰のことをL2正則化、Tikhonov正則化とも言う。
- ・Ridge回帰の解は解析的に書けるので嬉しい。
実際、Ridge回帰の行列表現:
$\displaystyle\min_w\|y-Xw\|^2_2+\lambda\|w\|^2_2$
の解は、
$w=(X^{\top}X+\lambda I)^{-1}X^{\top}y$
と書くことができます。
$\lambda=0$ の場合が普通の最小二乗法に対応します:
$w=(X^{\top}X)^{-1}X^{\top}y$
ElasticNet
Ridge と LASSO を混ぜたのが ElasticNet です。
$\displaystyle\min_w\sum(y-f(w,x))^2+\lambda_1\|w\|_1+\lambda_2\|w\|_2^2$
次回は 移動平均の意味と計算方法(時系列データ、画像処理で活躍) を解説します。
