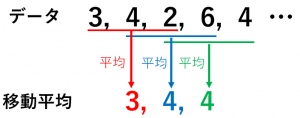
移動しながら順々に平均をとっていったものを移動平均と言います。
移動平均はどんなところに登場するか
「移動平均」の考え方は、
1.時系列データの分析
2.画像処理
に応用することができます。それぞれについて説明します。
時系列データに対する移動平均
時系列データに対して、直近の $n$ 個のデータの平均を計算して新しいデータとすることで、もとのデータの特徴を残したまま、ある程度滑らかなデータを得ることができます。この計算を移動平均と言います。
以下の時系列データに対して、移動平均を計算せよ(ただし、$n=3$ とする)。
$3,4,2,6,4,5,6,7,5,9,10,14,12,13$

解答
$3$ 個のデータの平均を順々に計算していきます。
最初は、$\frac{3+4+2}{3}=3$
次は、$\frac{4+2+6}{3}=4$
その次は、$\frac{2+6+4}{3}=4$
という感じです。全て求めると、
$3,4,4,5,5,6,6,7,8,11,12,13$
となります。
まさに移動しながら平均を取っていく感じです。なお、移動平均の計算方法は他にもたくさんありますが、今回扱った「直近の $n$ 個の平均を取る」という単純移動平均がスタンダードです。
画像処理における移動平均フィルタ
画像が「各ピクセルの値」として表現されているものとします。例えば、白黒画像で、数字が大きい部分は白、小さい部分は黒という感じです。
このとき、自分の「周囲」のマス目の平均値を計算したものが移動平均です。
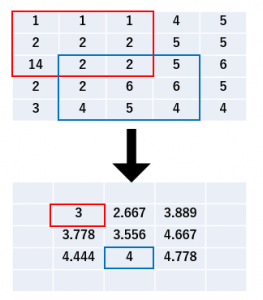
例として、5ピクセル×5ピクセルの画像に対する移動平均を計算したものを図に示します。
左上3×3部分の平均が、
$\dfrac{1+1+1+2+2+2+14+2+2}{9}=3$
となっています。他の部分も同様です。
移動平均の意味
先ほどの時系列データの具体例で確認してみましょう。青がもとの時系列データ、赤が移動平均後の時系列データです。
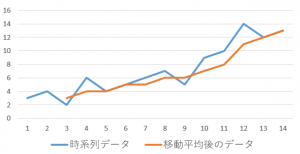
もとの時系列データは「時間の経過につれて徐々に値が増加していく」という特徴(増加トレンド)がありそうです。ですが、途中でギザギザしておりよく分かりません。移動平均を取ることで、増加トレンドがより明確になります!
画像処理の移動平均フィルタも同様の効果があります。つまり「もとの画像の特徴を持ちながらも、ある程度滑らかである画像」を得ることができます。「1ピクセルだけ異常な値が入ってしまった」というようなノイズの除去に使うことができます。
次回は 変動係数の計算方法と意味を分かりやすく解説 を解説します。
