球面集中現象

二次元の場合

いきなり高次元の球を考えるのは大変なので、二次元の場合の球（つまり円）について考えます。半径 $1$ の円について、中心から距離が $0.9$ 以上離れている部分を「表面付近」と呼ぶことにします（図の緑の部分です）。

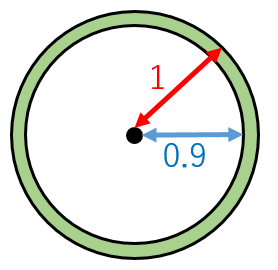
・全体の円の面積は $\pi\times 1^2=\pi$
・「表面付近」の面積は $\pi -\pi\times 0.9^2=0.19\pi$
つまり、全体のうち表面付近にあるのは $19$ ％です。

三次元の場合

次に、三次元の場合の半径1の球（つまり普通の球）について考えます。同様に、中心から距離が $0.9$ 以上離れている部分を「表面付近」とします。

二次元の場合と同様に直接計算してもOKですが、ここでは（三次元空間において）相似な図形の体積比が相似比の三乗に比例することを使って計算してみます。
・全体の球の体積を $V$ とおく
・「表面付近」の体積は $V-V\times 0.9^3=V(1-0.9^3)$
つまり、全体のうち表面付近にあるのは $1-0.9^3=0.271$→$27$ ％程度です。二次元の場合よりも「表面付近」の割合が増えました。

高次元の場合

四次元以上の場合は図形をイメージすることはできませんが、同様に計算することはできます。$n$ 次元空間における半径 $1$ の球について考えます。中心から距離が $0.9$ 以上離れている部分を「表面付近」とします。

・全体の球の体積を $V$ とおく
・「表面付近」の体積は $V-V\times 0.9^n=V(1-0,9^n)$
つまり、全体のうち表面付近にある部分の割合は $1-0.9^n$ です。

これは、$n$ が増えるとどんどん $1$ に近づきます：
$n=2$→$19$％
$n=3$→$27$％
$n=4$→$34$％
$n=5$→$41$％
$n=10$→$65$％
$n=15$→$79$％
$n=20$→$88$％

つまり、高次元空間の球では体積のほとんどが表面付近に集中していることになります。高次元空間ではメロンパンのほとんどは皮の部分という訳です。直感では理解しがたいおもしろい現象です。これを球面集中現象と言います。

次元の呪い

高次元空間では、球面集中現象のように我々の直感と反する現象が起こります。このことによって、統計や機械学習の手法（例えばサンプリングやクラスタリングなど）がうまくいかなくなることがあります。

このような「高次元であることによって現れるマイナスの効果」を次元の呪いと言います。

次回は いろいろな関数のn次導関数 を解説します。