区分求積法の意味と例題

区分求積法の公式は見た目が難しそうですが、一度理解してしまえば難しくありません。分かりやすく解説していきます。

区分求積法の公式とその導出

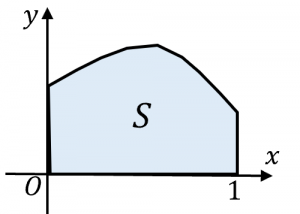
※ただし、$f(x)\geq 0$ とします。

まず、面積は定積分で計算できるので、上記の面積は
$S=\displaystyle\int_0^1 f(x)dx$
と表すことができます。

一方、図のように、$x=0$ から $x=1$ までの区間を $n$ 個に分割して、$n$ 個の長方形を作ってみましょう。

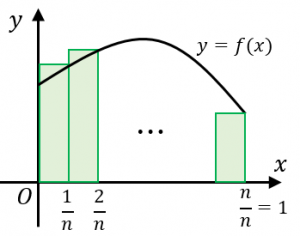
この長方形の面積を足し上げると、
$\dfrac{1}{n}f\left(\dfrac{1}{n}\right)+\dfrac{1}{n}f\left(\dfrac{2}{n}\right)+\cdots +\dfrac{1}{n}f\left(\dfrac{n}{n}\right)\\
=\displaystyle\sum_{k=1}^n\dfrac{1}{n}f\left(\dfrac{k}{n}\right)$
となります。

$n$ をどんどん増やしていくと、長方形の横幅はどんどん $0$ に近づいていくので、
長方形の面積の和 は $f(x)$ と $x$ 軸と $x=0$ と $x=1$ で囲まれた部分の面積に近づいていきます。

つまり、求める面積 $S$ は $\displaystyle\lim_{n\to\infty}\sum_{k=1}^n\dfrac{1}{n}f\left(\dfrac{k}{n}\right)$
と表すこともできます。

以上により、区分求積法の公式：
$\displaystyle\lim_{n\to\infty}\sum_{k=1}^{n}\dfrac{1}{n}f\left(\dfrac{k}{n}\right)$$=$$\displaystyle\int_0^1f(x)dx$
が成立することが分かりました。

区分求積法を使った例題

区分求積法は「たし算の極限」を積分に帰着させる手法です。区分求積法を使う例題として、以下の「たし算の極限」を計算してみましょう。

区分求積法
$\displaystyle\lim_{n\to\infty}\sum_{k=1}^{n}\dfrac{1}{n}f\left(\dfrac{k}{n}\right)$$=$$\displaystyle\int_0^1f(x)dx$
を使って計算してみます。

区分求積法を使う際には、和を $\sum\dfrac{1}{n}f\left(\dfrac{k}{n}\right)$ の形にするのがコツです。

$\dfrac{1^2+2^2+\cdots +n^2}{n^3}\\
=\dfrac{1}{n}\left(\dfrac{1^2}{n^2}+\dfrac{2^2}{n^2}+\cdots +\dfrac{n^2}{n^2}\right)\\
=\displaystyle\sum_{k=1}^n\dfrac{1}{n}f\left(\dfrac{k}{n}\right)$
と変形できます。ただし、$f(x)=x^2$ です。

よって、上式で $\displaystyle\lim_{n\to\infty}$ の極限を取ると、区分求積法の公式
$\displaystyle\lim_{n\to\infty}\sum_{k=1}^{n}\dfrac{1}{n}f\left(\dfrac{k}{n}\right)=\int_0^1f(x)dx$
より、
$\displaystyle\int_0^1 x^2dx\\
=\left[\dfrac{1}{3}x^2\right]_0^1\\
=\dfrac{1}{3}$
となります。

区分求積法の応用：端の方は気にしない

区分求積法の公式：
$\displaystyle\lim_{n\to\infty}\sum_{k=1}^{n}\dfrac{1}{n}f\left(\dfrac{k}{n}\right)=\int_0^1f(x)dx$
において、シグマの部分（和の範囲）を少し変えた

$\displaystyle\lim_{n\to\infty}\sum_{k=0}^{n-1}\dfrac{1}{n}f\left(\dfrac{k}{n}\right)=\int_0^1f(x)dx$
や
$\displaystyle\lim_{n\to\infty}\sum_{k=4}^{n+12}\dfrac{1}{n}f\left(\dfrac{k}{n}\right)=\int_0^1f(x)dx$
のような式も成り立ちます。

理由：
「微小な長方形を無数に足す」というイメージなので、端っこの長方形が多少増えたり減ってもその値に影響はありません。

区分求積法を使わない場合もある

「たし算の極限」を計算する方法の1つが区分求積法ですが、区分求積法を使わなくても「たし算の極限」を直接計算できる場合もあります。

この問題はわざわざ区分求積法を使わなくても、
$1^2+2^2+\cdots +n^2=\dfrac{1}{6}n(n+1)(2n+1)$
という公式を使えば解けます。実際、
$\dfrac{1^2+2^2+\cdots +n^2}{n^3}\\
=\dfrac{1}{n^3}\cdot\dfrac{1}{6}n(n+1)(2n+1)\\
=\dfrac{1}{6}\left(1+\dfrac{1}{n}\right)\left(2+\dfrac{1}{n}\right)$
なので、$n\to\infty$ のときの極限値は $\dfrac{1}{3}$ になります。

次回は 加重平均（重みつき平均）の例と意味 を解説します。