それぞれの重要度を加味した平均を加重平均(重み付き平均)と言う。
加重平均を使う例(二つの場合)
二つの数字 $x_1$、$x_2$ に対して、
単純平均は $\dfrac{x_1+x_2}{2}$
加重平均(重要度を加味した平均)は $\dfrac{w_1x_1+w_2x_2}{w_1+w_2}$
です。ただし、$w_1$ は $x_1$ の重み(重要度)、$w_2$ は $x_2$ の重みを表します。
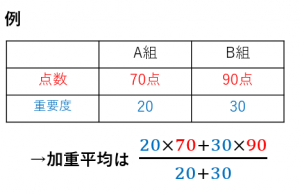
A組とB組でテストを行った。
A組の平均点は $70$ 点、B組の平均点は $90$ 点であった。全体の平均点はいくらか?
ただし、A組の人数は $20$ 人、B組の人数は $30$ 人とする。
答え
単純にクラス間の平均を計算すると、$\dfrac{70+90}{2}=80$ 点です。
しかし、クラスの人数に差があり、人数が多いクラスの方が重要(全体の平均点に与える影響が大きい)です。
そこで、加重平均を計算すると、
$\dfrac{20\times 70+30\times 90}{20+30}=\dfrac{4100}{50}=82$ 点となります。
B組(優秀なクラス)の人数が多いため、単純平均よりも加重平均(重みを考慮した場合)の方が高くなっています。
加重平均を使う例(三つ以上の場合)
$n$ 個の数字 $x_1,x_2,\cdots,x_n$ に対して、それぞれの重み(重要度)を $w_1,w_2,\cdots,w_n$ とします。このとき加重平均(重要度を加味した平均)は $\dfrac{w_1x_1+w_2x_2+\cdots +w_nx_n}{w_1+w_2+\cdots +w_n}$ と定義されます。
りんご(200円)、みかん(100円)、バナナ(60円)を売っているお店がある。このお店の商品の値段の平均はいくらか。
ただし、お店にはりんごが10個、みかんが5個、バナナが20本ある。
答え
単純に3つの商品の平均を計算すると、$\dfrac{200+100+60}{3}=120$ 円です。
しかし、商品の個数に差があり、商品が多い品物の方が重要(全体の平均点に与える影響が大きい)です。
そこで、加重平均を計算すると、
$\dfrac{10\times 200+5\times 100+20\times 60}{10+5+20}$
$=\dfrac{3700}{35}=105.7\cdots$
円となります。
加重平均の性質
重みが全て同じ場合は単純平均と一致する。
実際、$w_1=w_2=w$ のとき、
$\dfrac{x_1w_1+x_2w_2}{w_1+w_2}=\dfrac{x_1w+x_2w}{w+w}=\dfrac{x_1+x_2}{2}$
となり、単純平均と一致します。$n$ が $3$ 以上の場合も同様です。
加重平均はデータの最大値以下であり、データの最小値以上である。
例えば、$x_1=10,x_2=20,x_3=30$ のとき、重みがいくつであっても、加重平均は $10$ 以上 $30$ 以下になります。
次回は 期待値の意味と計算方法 を解説します。
