交流における実効値の意味とルート2が現れる理由

このページでは、実効値の意味と、実効値が最大値の $\dfrac{1}{\sqrt{2}}$ 倍になる理由について解説します。

電圧の実効値

正弦波交流について考えます。つまり、電圧が
$V=V_0\sin\dfrac{2\pi}{T} t$
と表される状況を考えます。この交流における電圧の最大値は $V_0$ です。

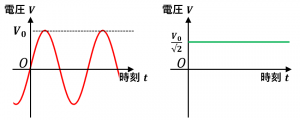
一方、同じ抵抗に対して、電圧が $\dfrac{V_0}{\sqrt{2}}\fallingdotseq 0.707V_0$ の直流を流してみます。すると、２つの状況の平均消費電力が同じになります（理由は後述）。

つまり「最大電圧が $V_0$ の正弦波交流と、電圧が $\dfrac{V_0}{\sqrt{2}}$ の直流は、消費電力の意味で同じ」と言えます。

これを、最大電圧が $V_0$ の正弦波交流の実効電圧は $\dfrac{V_0}{\sqrt{2}}$ である、などと言います。

電流の実効値

つまり「最大電流が $I_0$ の正弦波交流と、電流が $\dfrac{I}{\sqrt{2}}$ の直流は、消費電力の意味で同じ」と言えます。

以上をまとめると、電圧、電流いずれにせよ、実効値は最大値を $\sqrt{2}$ で割ったものと言うことができます。

ルート２が現れる理由

※「消費電力の意味で同じ」をもう少し正確に言うと「消費電力の平均が同じ」です。

まず、電圧が $\dfrac{V_0}{\sqrt{2}}$ の直流の消費電力は、$\dfrac{1}{2}RV_0^2$ になります。
参考：消費電力（ワット）を計算する３つの方法（電流、電圧、抵抗から）

次に、最大電圧が $V_0$ の正弦波交流の平均消費電力を計算すると、
$\dfrac{1}{T}\displaystyle\int_0^{T}RV^2dt$
$=\dfrac{1}{T}R\displaystyle\int_0^{T}(V_0\sin^2\dfrac{2\pi}{T}t)^2dt\\
=\dfrac{1}{T}RV_0^2\displaystyle\int_0^{T}\dfrac{1-\cos 2\cdot\frac{2\pi}{T}t}{2}dt\\
=\dfrac{1}{T}RV_0^2\cdot\dfrac{T}{2}\\
=\dfrac{1}{2}RV_0^2$
となり一致しました。

コンセントの電圧

一般的な家庭用コンセントの電圧は100Vです。これは、実効電圧が100Vという意味です。つまり、交流電圧の最大値は、およそ141.4Vになります。

実効値と平均値は異なる

実効値は「消費電力の意味での」平均です。電流や電圧の大きさ自身の平均値とは異なるので注意が必要です。

ちなみに、最大電圧が $V_0$ である正弦波交流の電圧の大きさの平均値は、$\dfrac{2}{\pi}V_0\fallingdotseq 0.637V_0$ になります。$\dfrac{1}{\sqrt{2}}\fallingdotseq 0.707$ なので、
平均値＜実効値＜最大値
であることが分かります。

次回は 複号同順と複号任意の意味 を解説します。