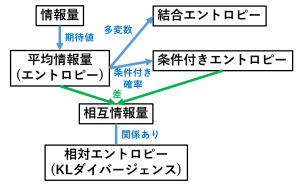
情報量、情報エントロピーに関連する重要な用語とその関係を整理しました。
定義式などは、離散型確率分布の場合で記述しています。連続型の場合は、$\Sigma$ を $\int$ に読み替えてください。
情報量とは
情報量の例:
確率 $\dfrac{1}{2}$ で起こる事象の情報量は、
$-\log_2\dfrac{1}{2}=1 ビット$
です。情報量の単位はビットです。
情報量の意味:
情報量は、文字通りその事象が起こったときに得られる情報の量と解釈できます(確率が低い事象が起こるのは珍しい!→情報量が多い、と解釈)。
「情報量」は「あいまいさ」や「不確実性」と表現することもあります。
平均情報量(情報エントロピー)とは
$H(X)=-\displaystyle\sum_{i=1}^np_i\log_2 p_i$
で定義します。
平均情報量のことを、情報エントロピーとも言います。
平均情報量の意味:
平均情報量は、その確率分布に従って1つのデータをサンプリングするときに、得られる情報量の期待値です。
結合エントロピーとは
結合エントロピーの意味:
情報エントロピーの多変数バージョンです。
(情報エントロピーの確率分布を同時確率分布にしたものです)
条件付きエントロピーとは
$H(Y\mid X)\\
=-\displaystyle\sum_{i=1}^mp(x_i)\sum_{j=1}^np(y_j\mid x_i)\log_2p(y_j\mid x_i)$
で定義します。
条件付きエントロピーの意味:
条件付きエントロピー $H(Y\mid X)$ は、「$X$ の値は知っているという状態から、$Y$ を新たに知ったときに得られる情報量 $-\log_2 p(y_j\mid x_i)$」の期待値です。
定義式を変形して $\displaystyle\sum_{i,j}p_{ij}\{-\log_2 p(y_j\mid x_i)\}$ と書くと分かりやすいかもしれません。
情報エントロピーの条件付き確率バージョンです。
相互情報量とは
$I(X,Y)=H(Y)-H(Y\mid X)$
で定義します。
相互情報量の定義式は対称です。つまり、$I(X,Y)=H(X)-H(X\mid Y)$ も成立します。また、相互情報量は必ず0以上です。
相互情報量の意味:
・相互情報量は「平均情報量」と「条件付きエントロピー」の差です。
・つまり「$Y$ の情報量」と「$X$ を知っている状態における $Y$ の情報量」の差です。
相対エントロピーとは
$-\displaystyle\sum_{i=1}^np_i\log\dfrac{q_i}{p_i}$
で定義します。
相対エントロピーのことを、KLダイバージェンスとも言います。相対エントロピーは、必ず $0$ 以上の値になります。
相対エントロピーの意味:
・相対エントロピーは「2つの確率分布がどれくらい異なるかを表す量」という解釈ができます。
・$P(X)P(Y)$ に対する $P(X,Y)$ の相対エントロピーが、相互情報量と一致します。
次回は 交差エントロピーの例と微分の計算 を解説します。
