ハードマージンSVM(サポートベクタマシン)でやりたいこと、および定式化の方法、結果を説明します。
問題設定
・2クラス分類問題を考えます。
・$N$ 個のデータ $(\overrightarrow{x_i},y_i)\:(i=1,\dots, N)$ が与えられている状況を考えます。
・$\overrightarrow{x_i}$ は説明変数です。
・$y_i$ は教師ラベルです。クラス1に属するデータでは $y_i=1$ で、クラス2に属するデータでは、$y_i=-1$ です。
SVM でやりたいこと
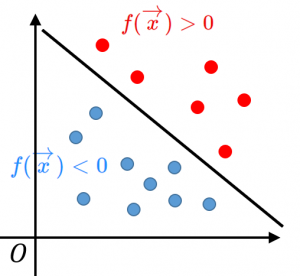
条件1:$f(\overrightarrow{x})>0$ ならクラス1と判定し、$f(\overrightarrow{x})<0$ ならクラス2と判定する。この方法で、与えられた全てのデータをきちんと判別できる。
条件2:条件1を満たす $f$ の中で、超平面 $f(\overrightarrow{x})=0$ から一番近い点までの距離が最大になる(自信を持って判別するために、境界面ギリギリにデータがいない方が嬉しいので)。
定式化の結果
$i=1,\dots, N$ について、$y_i(\overrightarrow{w}\cdot\overrightarrow{x_i}+b)\geq 1$
という制約条件のもとで、
$\|\overrightarrow{w}\|_2^2$ を最小化する(ような $\overrightarrow{w}$ と $b$ を求める)。
導出
条件1(正しく判別できる)は、
$y_i(\overrightarrow{w}\cdot\overrightarrow{x_i}+b)>0\:(i=1,\dots,N)$
と書けます。
条件2(マージン最大化)は、点と直線の距離公式(の高次元バージョン)を使うと、
$\displaystyle\min_{i}\dfrac{|\overrightarrow{w}\cdot\overrightarrow{x_i}+b|}{\|\overrightarrow{w}\|_2}$ を最大化する
と書けます。
ここで、$\overrightarrow{w}$ と $b$ を同じ定数倍しても、識別面が変わらないことに注意すると、
$\displaystyle\min_{i}|\overrightarrow{w}\cdot\overrightarrow{x_i}+b|=1$
という(正規化っぽい)条件を追加しても、得られる識別面は同じであることが分かります。
このとき、条件2は $\dfrac{1}{\|\overrightarrow{w}\|_2}$ を最大化する、と同値です。さらに、これは、$\|\overrightarrow{w}\|_2^2$ を最小化する、と同値です。
そして、条件1かつ追加した制約条件を満たすことは、以下の2つの条件を満たすこと同値です:
条件A
$y_i(\overrightarrow{w}\cdot\overrightarrow{x_i}+b)\geq 1\:(i=1,\dots,N)$
条件B
$|\overrightarrow{w}\cdot\overrightarrow{x_i}+b|=1$ となる $i$ が存在する。
さらに、条件Aのもとで $\|\overrightarrow{w}\|_2^2$ を最小化すると、自動的に条件Bは満たされる(満たされない場合、$\overrightarrow{w}$ と $b$ を $(1-\varepsilon)$ 倍することで、よりよい解を得られてしまう)ので、条件Bは省くことができます。
結局条件Aのもとで $\|\overrightarrow{w}\|_2^2$ を最小化することで、条件1と条件2を満たす識別面を得ることができます。
次回は ニューラルネットワークの仕組みと応用例を簡単に解説 を解説します。
