グラフを表すデータ構造である「隣接行列」と「隣接リスト」について解説します。
グラフを表すデータ構造
下図のようなネットワークっぽいものをグラフと言います(正確には頂点集合と辺集合のペアをグラフと言います)。
これを表現するデータ構造として隣接行列と隣接リストというものがあります。
図のようなグラフを隣接行列、隣接リストそれぞれで表現してみます:
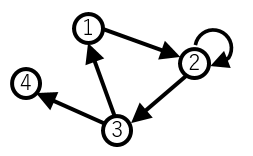
隣接行列
$\begin{pmatrix}0&1&0&0\\0&1&1&0\\1&0&0&0\\0&0&0&0\end{pmatrix}$
辺があるところに $1$、ないところに $0$ を格納した行列です。例えば、頂点 $1$ から頂点 $2$ へ辺があるので、$12$ 成分($1$ 行目の $2$ 列目)が $1$ となっています。
隣接行列は、プログラム上では二次元配列で実現できます。
隣接リスト
$1\to$「$2$」というリスト
$2\to$「$2,3$」というリスト
$3\to$「$1$」というリスト
$4\to$ 空のリスト
各頂点について、自分から出ている辺の行き先をリスト化して表現したものです。例えば、頂点 $2$ からは頂点 $2$ と $3$ に行けるので「$2,3$」というリストを持っています。
隣接行列と隣接リストの比較
隣接行列による表現は
×メモリが $|V|\times |V|$ くらい必要
○定数時間で特定の辺があるかどうか判定できる
×次数(特定の頂点から出ている辺の数)を求めるのが少し遅い
○隣接行列のかけ算や、固有値が意味を持つこともある
隣接リストによる表現は
○メモリが $|E|$ くらいあればよい(辺が少ないグラフでは有利)
×特定の辺があるかどうかの判定に、最悪 $O(|V|)$ の時間がかかる
○次数を求めるのが少し速い
それぞれに長所と短所があるので、やりたいことに応じてデータ構造を使い分けましょう。
余談
・無向グラフも同様に、隣接行列でも隣接リストでも表現できます。
・多重辺も扱えます。
隣接行列では、例えば各成分を辺の数とすれば表現できます。
隣接リストでは、同じ番号の重複を許せば表現できます。
・重み付きグラフも表現できます。
隣接行列では、例えば各成分を重みとすれば表現できます(多重辺かつ重み付きの場合は少し困りますが)。
隣接リストでは「行き先と重みのペアのリスト」を持てば表現できます。
次回は 有向非巡回グラフ(DAG)の意味とトポロジカルソート を解説します。
