有向非巡回グラフ(DAG)について、意味や性質を説明します。
有向非巡回グラフとは
有向とは、枝に向きがあることを表します。
また、非巡回とは、有向サイクル(矢印の向きにたどって一周できるようなサイクル)が無いことを表します。
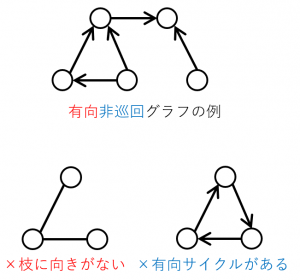
有向非巡回グラフは英語で Directed Acyclic Graph と言うので、頭文字を取って DAG(ダグ)と呼ばれることも多いです。
DAG は、例えば複数のタスクの依存関係などを表現することができます。
トポロジカルソート
このような番号づけで、どの矢印についても、行き先の番号が根本の番号より大きくなるようなものをトポロジカルソート(またはトポロジカルオーダー)と言います。
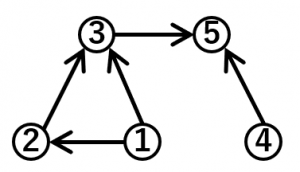
先ほど紹介した DAG に対しては、例えば図のようなトポロジカルソートが可能です。例えば、タスクの依存関係を表す例におけるトポロジカルソートは「どのような順番でタスクをこなせばよいか」の答えの1つと考えることができます。
トポロジカルソートが可能 $\iff$ $G$ は DAG
という性質があります。
$\Rightarrow$ は(対偶を考えると)簡単に分かります。実際、有向サイクルがあったら、そのサイクルのどこかで、大小関係が逆転するので、トポロジカルソートは不可能です。
トポロジカルソートのアルゴリズム
次は、上記の性質の $\Leftarrow$ について考えてみます。
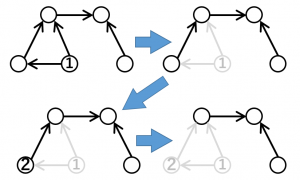
入ってくる枝がない頂点を1つ選んで1番をつける
→1番の頂点と、1番につながっている枝を除く
→入ってくる枝がない頂点を1つ選んで2番をつける
→2番の頂点と、2番につながっている枝を除く
→入ってくる枝がない頂点を1つ選んで3番をつける
→以下同様
という、非常に簡単なアルゴリズムでトポロジカルソートを与えることができます。
※実際、全ての枝が最終的に除かれますが、除かれるタイミングでは根本の頂点は番号づけされていて、行き先の頂点には番号づけされていません。つまりどの矢印についても、行き先の番号が根本の番号より大きくなるという性質が確かに満たされています。
※一般に、同じグラフに対するトポロジカルソートは何種類もあります。
※アルゴリズムのどの段階でも「入ってくる枝がない頂点」を選ぶことができます。そのような頂点が存在しないグラフには有向サイクルが含まれるからです。
DAG の他の性質
・DAG に対して、
頂点 $v$ から $w$ へのパスが存在する $\iff$ $v\leq w$
という規則で二項関係 $\leq$ を定めると、$\leq$ は半順序になります。実際、反射律、推移律、反対称律が簡単に確認できます。
関連:半順序集合と全順序集合の意味と例
・トポロジカルソートは、この半順序を(比較不能なものも比較できるようにして)全順序に拡張したもの、とみなすことができます。
・有向グラフ $G$ について、
$G$ 強連結成分分解したときに、全ての連結成分が1つの頂点からなる
$\iff$ $G$ は DAG
が成立します。
次回は ナップサック問題を動的計画法で解く を解説します。
