混合ガウス分布（GMM）の意味と役立つ例

混合ガウス分布の意味と、役立つ例について整理しました。

混合ガウス分布とは

ただし、$N(x\mid\mu_k,\Sigma_k)$ は平均が $\mu_k$ で分散共分散行列が $\Sigma_k$ であるガウス分布（の確率密度関数）とします。

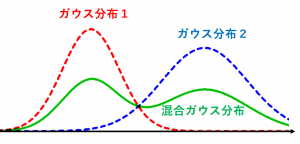
図の説明：
ガウス分布１とガウス分布２を $\pi_1=\pi_2=0.5$ の割合で混ぜた混合ガウス分布。このように、混合ガウス分布は多峰性の分布を表現できます。

$\pi_k$ は混合の割合を表す係数で、$\displaystyle\sum_{k=1}^K\pi_k=1$ を満たします。

混合正規分布、GMM、Gaussian Mixture Model などとも言います。

混合ガウス分布は何の役に立つか？

混合前の「もとのガウス分布」それぞれをクラスタに対応させます。具体的には、以下のようにクラスタリングを行います。

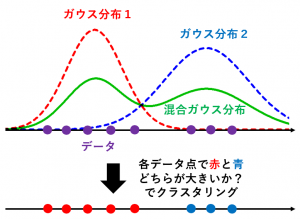
1. クラスタリング対象のデータ $x_1,x_2,\dots,x_n$ が与えられたとする
2. そのデータを生成していそうな混合ガウス分布を推定する
3. 各点で「どのガウス分布の密度が大きいか」によってクラスタリングを行う

※図は一次元ですが、多次元の場合も同様です。

※上記の手順では、各データは1つのクラスタに対応づけられます（ハードクラスタリング）。手順3において、混合前のそれぞれの割合（負担率）を出力とみなせば「各データが各クラスタに属する重み」を出力することもできます（ソフトクラスタリング）。

混合ガウス分布のパラメータ推定

これは、単純に最尤推定をすれば良さそうです。つまり、
$p(x)=\displaystyle\sum_{k=1}^K\pi_kN(x\mid\mu_k,\Sigma_k)$
として、$\displaystyle\prod_{i=1}^np(x_i)$ を最大にするようなパラメータ（$\pi_k,\mu_k,\Sigma_k$）を決めれば良さそうです。

しかし、そのような（$\pi_k,\mu_k,\Sigma_k$）は解析的な式を使ってきれいに表すことができないため、EMアルゴリズムという手法を使って数値的に計算されます。

負担率とは

混合ガウス分布が与えられたとき、「$x_i$ における $k$ 番目のガウス分布の割合」を負担率と言います。

具体的には、負担率 $\gamma_{ik}$ は以下の式で表すことができます。
$\gamma_{ik}=\dfrac{\pi_kN(x_i\mid \mu_k,\Sigma_k)}{\displaystyle\sum_{k=1}^K \pi_kN(x_i\mid \mu_k,\Sigma_k)}$

EMアルゴリズムの概要

求めたいパラメータ（$\pi_k,\mu_k,\Sigma_k$）は、負担率の簡単な関数で表すことができます：
$\pi_k=f_1(\gamma_{ik})$
$\mu_k=f_2(\gamma_{ik})$
$\Sigma_k=f_3(\gamma_{ik})$

（負担率もパラメータに依存しているため、上記の式は $x=f(x)$ のような方程式です）

そこで、上記の方程式を反復法で解きます：
1. パラメータ（$\pi_k,\mu_k,\Sigma_k$）を適当に決める
2. 現在のパラメータに従って、負担率 $\gamma_{ik}(i=1,\dots, n,k=1,\dots, K)$ を計算
3. 現在の負担率に従って、パラメータを計算
4. 以下、2と3を収束するまで繰り返す

次回は 1σ、2σ、3σの意味と正規分布の場合の確率 を解説します。