ローレンツ曲線とジニ係数

このページでは「どれくらい格差があるか」「どれくらい偏っているのか」を表すローレンツ曲線やジニ係数について詳しく解説します。

ローレンツ曲線とは

例えば「国民の所得にどれくらい格差があるか」をローレンツ曲線で表現すると、下図のようになります。

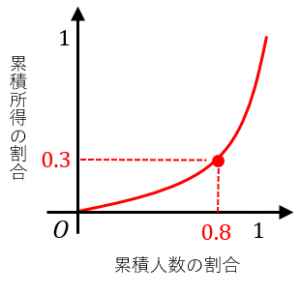
例えば、ローレンツ曲線が $(0.8,0.3)$ を通る時、
貧しい $80$ ％の人が全体の $30$ ％の富を持っている
ことを表します。

より一般には、
ローレンツ曲線が $(x,y)$ を通る $\iff$「貧しい側の割合 $x$ の人で全体の $y$ の富を持っている」
と言えます。

ローレンツ曲線の両端は必ず $(0,0)$ と $(1,1)$ です（パーセントで表す場合は $(1,1)$ ではなく $(100,100)$ になります）。また、ローレンツ曲線は右上がりです（単調非減少です）。

ローレンツ曲線と格差

ローレンツ曲線は右下にあればあるほど格差が大きいと言えます。

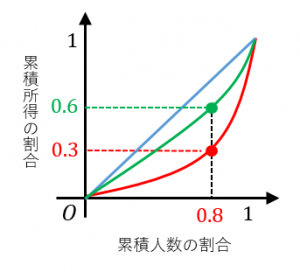
実際、
貧しい8割の人を集めても全体の3割の富しか持っていない
という状況の方が
貧しい8割の人を集めれば全体の6割の富を持っている
という状況よりも格差が大きいですね。

最も偏っていない状況は、全ての人が同じ富を持っている状況です。つまり、全ての $x$ について
「貧しい側の割合 $x$ の人で全体の $x$ の富を持っている」
ことになるので、ローレンツ曲線は $y=x$ になります。この線分を均等分配線と言います。

つまり、ローレンツ曲線が均等分配線から右下に離れれば離れるほど格差が大きい分布となります。

ジニ係数

「ローレンツ曲線がどれくらい右下にあるか」を具体的な数字で表現したものがジニ係数です。

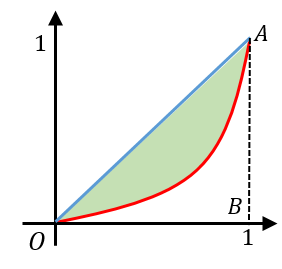
ジニ係数は、
均等分配線とローレンツ曲線で囲まれた部分の面積÷直角二等辺三角形 $OAB$ の面積
で定義されます。
（直角二等辺三角形 $OAB$ の面積は $\dfrac{1}{2}$ です）

・ジニ係数は $0$ 以上 $1$ 以下です。
・完全に平等なとき、つまりローレンツ曲線が均等分配線と一致するときは、ジニ係数は $0$ になります。
・最も格差が大きいとき、つまりローレンツ曲線が右下に張り付いているときは、ジニ係数は $1$ になります。

次回は Jaccard係数、Dice係数、Simpson係数 を解説します。