現在の $1000$ 円と将来の $1000$ 円は価値が違います。現在価値、将来価値について解説します。
将来価値とは
例えば、今 $1000$ 円持っていて、年利 $5$ パーセントで運用すると、1年後には $1050$ 円になります。$50$ 円増えました。
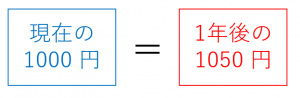
このように、今持っているお金は、将来のある時点では、より大きな価値を持っていると考えることができます。この考えのもと、今のお金が将来の時点でどのくらいの額にあたるのかを表すのが将来価値(Future Value, FV)です。
例えば、先ほど確認したように、現在の $1000$ 円は(利率 $5$ パーセントとすると)1年後の将来価値は $1050$ 円です。
より一般に、現在の $A$ 円は、利率を $r$ とすると、$n$ 年後の将来価値は $A(1+r)^n$ になります。
現在価値とは
さきほど確認したように、今持っているお金は、将来のある時点では、より大きな価値を持っていると考えられます。では、1年後の $1000$ 円は、今の何円と同じ価値でしょうか?
実は、
$952\times 1.05\fallingdotseq 1000$
なので、約 $952$ 円を年利 $5$ パーセントで運用すると1年後には $1000$ 円になります。
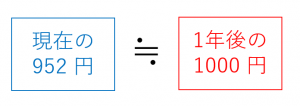
つまり、1年後の $1000$ 円は(年利 $5$ パーセントなら)現在の $952$ 円と同じ価値と考えることができます。このように、将来もらえるお金が、今の時点でどのくらいの額にあたるのかを表すのが現在価値(Present Value, PV)です。
一般に、利率を $r$ とすると、$n$ 年後の $A$ 円の現在価値は $A\div (1+r)^n$ になります。
割引率とは
現在価値を求めるときの計算に使う利率 $r$ のことを割引率と言います。
つまり、さきほどの式
現在価値 $=$ 将来のお金 $\div(1+r)^n$
に登場する $r$ のことを割引率と言います。
余談
・割引率が大きいほど
・期間が長いほど
現在のお金の価値と将来のお金の価値の差は大きくなります。そのため、きちんと現在価値・将来価値について考える必要があります。
逆に、利率がほぼ $0$ で、期間も短い場合は、現在のお金の価値と将来のお金の価値はほぼ一致します。
次回は 定率法による減価償却費計算の3つのポイント を解説します。
