${}_5\mathrm{C}_2=\dfrac{5\times 4}{2\times 1}=10$
${}_m\mathrm{C}_n$ は $m$ 個の異なるものから $n$ 個選ぶ方法(組合せ)の数です。
コンビネーションの計算例
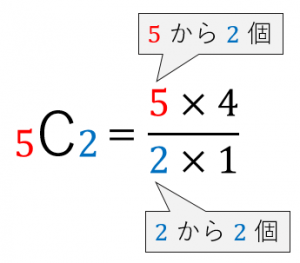
分子は、$5$ からはじめて $2$ 個並べる
分母は、$2$ からはじめて $2$ 個並べる
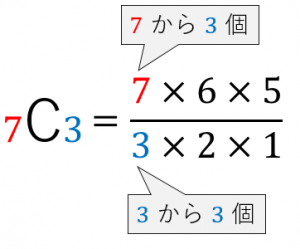
分子は、$7$ からはじめて $3$ 個並べる
分母は、$3$ からはじめて $3$ 個並べる
分子は、$3$ からはじめて $1$ 個並べる
分母は、$1$ からはじめて $1$ 個並べる
分子は、$2$ からはじめて $2$ 個並べる
分母は、$2$ からはじめて $2$ 個並べる
などとなります。
計算ツール
コンビネーションの計算をしてくれるサイトの使い方を解説します。検算に使えます。
例えば、${}_5\mathrm{C}_2$ というコンビネーションの値を計算したいときには、
wolframalpha.comにアクセスし、
combination(5,2)
と入力してみてください。
一般的な式
分子は、$m$ からはじめて $n$ 個並べる
分母は、$n$ からはじめて $n$ 個並べる
と覚えましょう。
階乗で表す
${}_m\mathrm{C}_n=\dfrac{m\times (m-1)\times \cdots \times (m-n+1)}{n\times (n-1)\times \cdots \times 2\times 1}$
の分母は、$1$ から $n$ までのかけ算なので、$n$ の階乗です。
参考:階乗の意味と値一覧など
つまり、
${}_m\mathrm{C}_n=\dfrac{m\times (m-1)\times \cdots \times (m-n+1)}{n!}$
と書くことができます。
さらに、この式の分母と分子に、
$(m-n)!=(m-n)\times(m-n-1)\times\cdots\times 1$
をかけると、分子は $m!$ になるので、
${}_m\mathrm{C}_n=\dfrac{m!}{n!(m-n)!}$
となることが分かります。
次回は 相関係数(定義式、意味、求め方) を解説します。
