コイン投げに関する確率のいろいろな問題

コイン投げに関する確率の練習問題を３問解説します。

全て同じ結果になる確率

解答：
コインを３枚投げたときのパターンは、
表表表
表表裏
表裏表
表裏裏
裏表表
裏表裏
裏裏表
裏裏裏
の８通りで、全て表となるのは、そのうちの１つです。

よって、全て表となる確率は、$\dfrac{1}{8}$ です。

特定の回数表が出る確率

解答：
コインを５回投げたときに出るパターンの数は、
$2^5=32$ です。

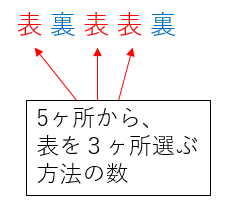
そのうち、３回表が出る場合の数を求めてみましょう。
これは「表が出る場所を３ヶ所選ぶ方法」の数と同じなので、
${}_5\mathrm{C}_3$ 通りです。

よって、求める確率は、
$\dfrac{{}_5\mathrm{C}_3}{32}=\dfrac{10}{32}=\dfrac{5}{16}$
となります。

期待値

解答：
例題２と同じようにして、コインを６回投げたときに表が $t$ 回出る確率は
$\dfrac{{}_6\mathrm{C}_t}{2^6}$
となります。

よって、表が出る回数の期待値は、
$\begin{aligned}&\displaystyle\sum_{t=0}^6 t\cdot\dfrac{{}_6\mathrm{C}_t}{2^6}\\&=\dfrac{1\cdot 6+2\cdot 15 +3\cdot 20 +4\cdot 15+5\cdot 6 +6}{64}\\&=\dfrac{6+30+60+60+30+6}{64}\\&=\dfrac{192}{64}\\&=3\end{aligned}$
となります。

次回は 確率における独立と従属の意味と例 を解説します。