分配法則の意味と図を使った説明

このページでは、分配法則の使い方や、分配法則の図を使った説明などを解説します。

分配法則を使った例題

$11\times 301=11\times(300+1)$
です。よって、
$11\times(300+1)$
を計算しましょう。分配法則：
$a\times (b+c)=a\times b+a\times c$
で $a=11$、$b=300$、$c=1$ とすると、
$11\times(300+1)=11\times 300+11\times 1$
となります。この右辺を計算すると、
$3300+11\\
=3311$
となります。

分配法則を図で説明

縦の長さが $a$、横の長さが $b+c$ である長方形の面積を考えてみます。

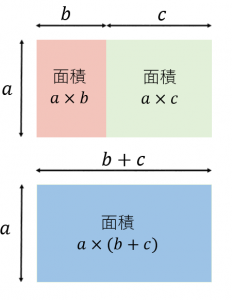
大きな長方形の面積を、二つに分けて考えると
$a\times b$ + $a\times c$ になり、

まとめて考えると $a\times (b+c)$ となります。

どちらも同じものを表しているので、結局
$a\times (b+c)=a\times b+a\times c$
という分配法則が成立します。

分配法則は2つある

分配法則として
$a\times (b+c)=a\times b+a\times c$
を紹介しました。実は、
$(a+b)\times c=a\times c+b\times c$
も成立します。これも分配法則と言います。

分配法則を使って式のかっこを外すことを、展開すると言います。

分配法則の証明

$a\times(b+c)$
は、$(b+c)$ を $a$ 個足したもの です。

足し算の順番は入れ替えられるので、これは $b$ を $a$ 個足したものと $c$ を $a$ 個足したものの合計です。

つまり $a\times (b+c)$ は $a\times b$ と $a\times c$ の合計です。

※厳密には分配法則は実数の公理なので「証明」という言葉は不適切かもしれません。

なお、分配法則は小学生で習いますが、中学数学、高校数学でも式を展開するときに、繰り返しお世話になります。

割り算バージョン

つまり、
$a\div (b+c)=a\div b+a\div c$
は成立しませんが、
$(a+b)\div c=a\div c+b\div c$
は成立します。

分数の形で書くと、$\dfrac{a}{b+c}=\dfrac{a}{b}+\dfrac{a}{c}$ は間違いで、$\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}$ は正しいというわけです。

次回は 交換法則、結合法則、分配法則 を解説します。