微分係数の定義と２つの意味

微分係数の定義、計算例、意味について整理しました。

微分係数の定義

関数 $f(x)$ に対して、
$\displaystyle\lim_{h\to 0}\dfrac{f(a+h)-f(a)}{h}$
という極限が存在するとき、その値を $x=a$ における $f(x)$ の微分係数と言い、$f'(a)$ と書きます。

解答：
$a=1$ として、
$\displaystyle\lim_{h\to 0}\dfrac{f(1+h)-f(1)}{h}\\
=\displaystyle\lim_{h\to 0}\dfrac{(1+h)^2-1^2}{h}\\
=\displaystyle\lim_{h\to 0}\dfrac{2h+h^2}{h}\\
=2$
つまり、微分係数は、$f'(1)=2$
となります。

１．接線の傾き

微分係数 $f'(a)$ は、$y=f(x)$ の $x=a$ における接線の傾きを表します。

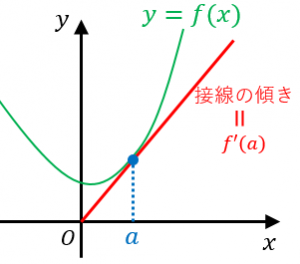
理由を考えてみましょう。

まず「$(a,f(a))$ と $(a+h,f(a+h))$ という２点を結ぶ直線 $l$」
を考えて、$h$ をどんどん $0$ に近づけていくと、接線に限りなく近づいていきます。

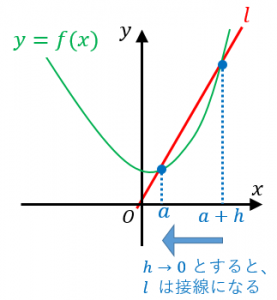
また、$l$ の傾きは、
$\dfrac{f(a+h)-f(a)}{(a+h)-a}=\dfrac{f(a+h)-f(a)}{h}$
です。

よって、接線の傾きは、
$\displaystyle\lim_{h\to 0}\dfrac{f(a+h)-f(a)}{h}$
となります。

これは微分係数 $f'(a)$ の定義と一致します！

２．瞬間の速度

理由を考えてみましょう。

時刻 $a$ から $a+h$ の間に移動した距離は、$f(a+h)-f(a)$ です。

よって、時刻 $a$ から $a+h$ の間の平均の速度は、移動距離÷時間なので、
$\dfrac{f(a+h)-f(a)}{(a+h)-a}=\dfrac{f(a+h)-f(a)}{h}$
となります。

ここで、時間 $h$ をどんどん $0$ に近づけていくと、平均の速度は時刻 $a$ における瞬間の速度に限りなく近づいていきます。

よって、時刻 $a$ における瞬間の速度は、
$\displaystyle\lim_{a\to 0}\dfrac{f(a+h)-f(a)}{h}$
となります。

これは微分係数 $f'(a)$ の定義と一致します！

次回は 関数の微分を自動で計算してくれるツール を解説します。