ベータ分布と他の分布のおもしろい3つの関係

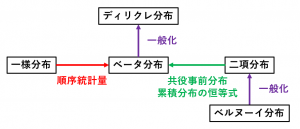
このページでは、ベータ分布という確率分布と、他の分布（一様分布、二項分布）のおもしろい関係について紹介します。

ベータ分布とは

そもそもベータ分布とは、確率密度関数が
$f_{\alpha,\beta}(x)=\dfrac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$
で表される分布です。少し難しそうな関数です。

$\alpha,\beta$ はベータ分布のパラメータ(正の実数)です。$\alpha,\beta$ を変えると、分布の形が変わります。
$x$ のとりうる値の範囲は $0\leq x\leq 1$ です。
$B(\alpha,\beta)$ はベータ関数です。$\alpha,\beta$ が正の整数のとき、$B(\alpha,\beta)=\dfrac{(\alpha-1)!(\beta-1)!}{(\alpha+\beta-1)!}$ となります。

ベータ分布と一様分布の関係

もう少し正確に言うと、
「 $[0,1]$ 上の一様分布から、独立に $\alpha+\beta-1$ 個を抽出したときの、小さい方から $\alpha$ 個目の値」が従う確率分布が、ベータ分布 $f_{\alpha,\beta}(x)$ になります。

証明は少し大変ですが「一様分布の順序統計量」などで検索すると、情報が得られます。

ベータ分布と二項分布の関係1

ベータ分布は二項分布の共役事前分布になります。ベータ分布が有名でよく使われるのは、この性質のおかげと言えるでしょう。

なお、二項分布は、$N$ 回のコイン投げで表が出る回数の分布です。$N=1$ のときがベルヌーイ分布です。つまり、ベータ分布はベルヌーイ分布の共役事前分布、と言うこともできます。

詳細は、共役事前分布の意味といくつかの例で解説しています。

ベータ分布と二項分布の関係2

ただし、$\alpha,\beta, x$ は正の整数です。
$F^{\mathrm{Beta}}_{\alpha,\beta}(x)$ はベータ分布の累積分布関数です。
$F^{\mathrm{Bin}}_{N,p}(n)$ は二項分布（確率 $p$ で表が出るコインを $N$ 回投げたときに表が出る回数の分布）の累積分布です。

3つの性質の中で、最も知られていないですが、非常におもしろい式です。

$[0,1]$ 上の一様分布から、独立に $\alpha+\beta-1$ 個を抽出します。

このとき、さきほど紹介したベータ分布と一様分布の関係を使うと、$F^{\mathrm{Beta}}_{\alpha,\beta}(x)$ は小さい方から $\alpha$ 個目が $x$ 以下である確率となります。

一方、小さい方から $\alpha$ 個目が $x$ より大きい確率は、確率 $x$ で表が出るコインを $\alpha+\beta-1$ 回投げたときに表が出る回数が $\alpha$ 回未満である確率と等しいです（※）。この確率は、$F^{\mathrm{Bin}}_{\alpha+\beta-1,x}(\alpha-1)$ そのものです。

以上の2つの確率を加えると1になるので、目的の式が成立します。

※理解するのが難しいポイントです。一様乱数が $x$ 以下 $\iff$ コインは表　のように対応させると分かりやすいです。

次回は パレート分布の意味、期待値、分散 を解説します。