2つのベクトル $\overrightarrow{a}$、$\overrightarrow{b}$ の足し算 $\overrightarrow{a}+\overrightarrow{b}$ について解説します。「図」および「成分表示」それぞれ理解しましょう。
図で理解する
2つのベクトル $\overrightarrow{a}$、$\overrightarrow{b}$ が与えられたとき、それらを加えたベクトル $\overrightarrow{a}+\overrightarrow{b}$ を図示してみましょう。
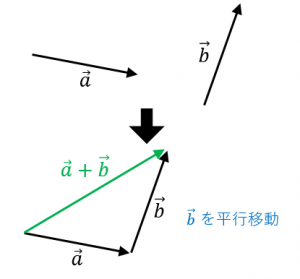
手順1:
2本の矢印のうち(どちらでもよい)片方の始点をもう片方の終点に持ってきます(平行移動します)。
手順2:
つながった2本の矢印の「全体の始点」から「全体の終点」へ伸ばした矢印が、求めたいベクトル $\overrightarrow{a}+\overrightarrow{b}$ となります。
ポイント:ベクトルは向きと大きさのみで定まります。どこにあるかは関係ないので平行移動してもOKです。
成分表示(座標)で理解する
成分表示された2つのベクトル $\overrightarrow{a}=(a_1,a_2)$、$\overrightarrow{b}=(b_1,b_2)$ の足し算は、
$\overrightarrow{a}+\overrightarrow{b}=(a_1+b_1,a_2+b_2)$
となります。つまり、それぞれの成分ごとに普通の足し算をすればベクトルの足し算になります。
例:$\overrightarrow{a}=(1,2)$ と $\overrightarrow{b}=(3,4)$ の足し算は、
$\overrightarrow{a}+\overrightarrow{b}=(1+3,2+4)=(4,6)$
上記は平面ベクトルの場合ですが、空間ベクトルについても同様です。つまり、2つのベクトル $\overrightarrow{a}=(a_1,a_2,a_3)$、$\overrightarrow{b}=(b_1,b_2,b_3)$ の足し算は、
$\overrightarrow{a}+\overrightarrow{b}=(a_1+b_1,a_2+b_2,a_3+b_3)$
となります。
ベクトルの足し算と大きさ
2つのベクトルを加えてできたベクトル $\overrightarrow{a}+\overrightarrow{b}$ の大きさ(絶対値)はもとのベクトルの長さの足し算と一致するとは限りません。
つまり、多くの場合、
$|\overrightarrow{a}|+|\overrightarrow{b}|\neq |\overrightarrow{a}+\overrightarrow{b}|$
となります。
実は、一般に
$|\overrightarrow{a}|+|\overrightarrow{b}|\geq |\overrightarrow{a}+\overrightarrow{b}|$
が成立します。この不等式を三角不等式と言います。
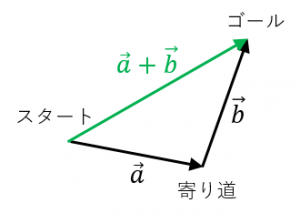
これは、図においてスタートからゴールまで行くのに、直線で行くほうが寄り道をするよりも近い(遠くはない)ことを表しています。
次回は 方向ベクトルの意味と2通りの求め方 を解説します。
