アフィン変換の意味と、アフィン変換の4つの基本要素について、2次元の場合の例を中心に詳しく解説します。
アフィン変換とは
アフィン変換は、一次変換に平行移動を加えたものです。
中学数学で習う比例 $y=ax$ を一般化したものが線形変換(一次変換)で、1次関数 $y=ax+b$ を一般化したものがアフィン変換です。
2次元のアフィン変換
二次元のアフィン変換は、行列 $A=\begin{pmatrix}p&q\\r&s\end{pmatrix}$ と平行移動を表すベクトル $b=\begin{pmatrix}b_1\\b_2\end{pmatrix}$ を用いて、以下のように表せます。
$\begin{pmatrix}y_1\\y_2\end{pmatrix}=\begin{pmatrix}p&q\\r&s\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}+\begin{pmatrix}b_1\\b_2\end{pmatrix}$
$A$ と $b$ を1つにまとめて、
$\begin{pmatrix}y_1\\y_2\\1\end{pmatrix}=\begin{pmatrix}p&q&b_1\\r&s&b_2\\0&0&1\end{pmatrix}\begin{pmatrix}x_1\\x_2\\1\end{pmatrix}$
と表すこともできます。
アフィン変換の4つの例
アフィン変換で $A$ が単位行列の場合、変換は $x+b$ となり、単なる平行移動になります。
特に、原点を中心とした拡大・縮小は、対角行列 $D$ を使って $x\to Dx$ と表すことができます。一次変換であり、アフィン変換でもあります。
特に、原点を中心とした回転は、直交行列 $Q$ を使って、$x\to Qx$ と表すことができます。一次変換であり、アフィン変換でもあります。
2次元の場合は、
$Q=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}$
のように表せます。
せん断は上記の3つよりも少しイメージしにくいです。せん断変換とは、$x$ を「ある直線 $l$ からの符号付き距離に比例した量だけ、$l$ の向きに動かす」ような変換です。
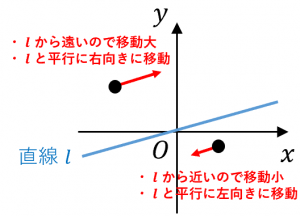
例えば、2次元で $l$ が $x$ 軸の場合、せん断変換は
$\begin{pmatrix}x\\y\end{pmatrix}\to \begin{pmatrix}1&a\\0&1\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}$
のように表すことができます。一次変換であり、アフィン変換でもあります。
アフィン変換の分解
これを証明してみます。まず、アフィン変換 $Ax+b$ に対して、$A$ を $QR$ 分解します。
つまり、$A=QR$(ただし $Q$ は直交行列で、$R$ は上三角行列)と分解します。(このような分解が存在することについては $QR$ 分解で調べてみてください)
すると、アフィン変換は、
$Ax+b\\
=Q\begin{pmatrix}r_{11}&r_{12}\\0&r_{22}\end{pmatrix}x+b\\
=Q\begin{pmatrix}r_{11}&0\\0&r_{22}\end{pmatrix}\begin{pmatrix}1&\frac{r_{12}}{r_{11}}\\0&1\end{pmatrix}x+b$
のように変形できます(※)。
$Q$ は回転、$\begin{pmatrix}r_{11}&0\\0&r_{22}\end{pmatrix}$ は拡大、$\begin{pmatrix}1&\frac{r_{12}}{r_{11}}\\0&1\end{pmatrix}$ は $x$ 軸方向のせん断、$b$ が平行移動ということで、4つの要素に分解できました。
証明の補足
※ $r_{11}=0$ の場合は、上記の変形はできないので、$Q\begin{pmatrix}1&\frac{r_{12}}{r_{22}}\\0&1\end{pmatrix}\begin{pmatrix}r_{11}&0\\0&r_{22}\end{pmatrix}x+b$
と変形すればOKです。
さらに $r_{22}=0$ の場合はこの変形もできませんが、その場合には、
$Q\begin{pmatrix}0&r_{12}\\0&0\end{pmatrix}x+b\\
=Q\begin{pmatrix}r_{12}&0\\0&0\end{pmatrix}\begin{pmatrix}0&1\\-1&0\end{pmatrix}x+b\\
=Q\begin{pmatrix}r_{12}&0\\0&0\end{pmatrix}\begin{pmatrix}\cos 270^{\circ}&-\sin 270^{\circ}\\\sin 270^{\circ}&\cos 270^{\circ}\end{pmatrix}x+b$
のように分解できます。
なお「アフィン変換を4つに分解できる」という言い方をしましたが「一次変換を3つ(回転、拡大、せん断)に分解できる」という言い方もできます。
次回は 相似変換の意味、表現行列や基底の変換行列との関係を整理 を解説します。
