微分の一般化である、劣微分について紹介します。
劣勾配と劣微分(一変数関数)
任意の $x$ に対して、
$f(x)\geq f(a)+c(x-a)$
を満たすような $c$ を、$x=a$ における $f$ の劣勾配と言います。
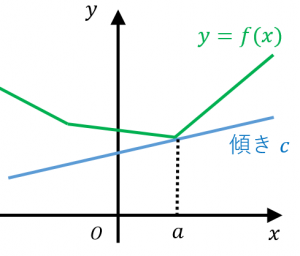
「関数 $f$ が $(a,f(a))$ を通る傾き $c$ の直線より上側にある」ような $c$ が劣勾配です。
また、劣勾配の集合(上記を満たす $c$ を全て集めた集合)を劣微分と言います。
具体例
例えば $y=|x|$ という関数について、$x=0$ における劣微分を求めてみましょう。
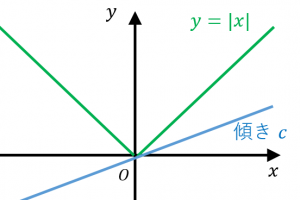
$(0,0)$ を通るいろいろな直線を書いてみると、
「関数 $y=|x|$ が $(0,0)$ を通る傾き $c$ の直線より上側にある」ような $c$ の集合は、$[-1,1]$ となります(閉区間)。
$0.2$ も、$1$ も、$-0.7$ も、全て $x=0$ における劣勾配です。
普通の微分と劣微分の関係
・微分可能なとき、普通の微分と劣微分は、ある意味で同じです。
$f$ の $x=a$ における劣微分が、要素数1の集合である場合、$f$ は $x=a$ で微分可能で、劣微分の要素と微分係数は一致します。
・微分不可能でも、劣微分は存在する(空集合でない)ことがあります。
例えば、上の例($y=|x|$ の $x=0$)では微分不可能な点で、劣微分が存在しています。
また、微分係数を用いた一次近似の式:
$f(x)\fallingdotseq f(a)+f'(a)(x-a)$
と、劣微分の定義の式:
$f(x)\geq f(a)+c(x-a)$
は似ています。
多変数関数の場合
任意の $\overrightarrow{x}$ に対して、
$f(\overrightarrow{x})\geq f(\overrightarrow{a})+\overrightarrow{c}^{\top}(\overrightarrow{x}-\overrightarrow{a})$
を満たすようなベクトル $\overrightarrow{c}$ を、$\overrightarrow{x}=\overrightarrow{a}$ における $f$ の劣勾配と言います。
これは、勾配ベクトル $\nabla f$ を用いた一次近似の式:
$f(\overrightarrow{x})\fallingdotseq f(\overrightarrow{a})+(\nabla{f}(a))^{\top}(\overrightarrow{x}-\overrightarrow{a})$
と似ています。
また、劣勾配の集合(上記を満たす $\overrightarrow{c}$ を全て集めた集合)を劣微分と言います。
次回は アークサイン、アークコサイン、アークタンジェントの微分 を解説します。
