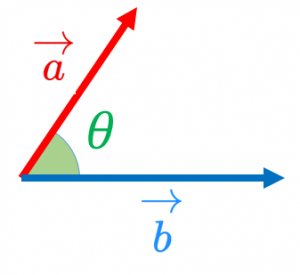
2つのベクトル $\overrightarrow{a}$ と $\overrightarrow{b}$ に対して、
$|\overrightarrow{a}||\overrightarrow{b}|\cos\theta$
のことを内積と言う。内積を $\overrightarrow{a}\cdot\overrightarrow{b}$ と書く。
内積の計算例
内積とは、
$|\overrightarrow{a}||\overrightarrow{b}|\cos\theta$
つまり、2つのベクトルの長さに、なす角の $\cos$ をかけたものです。
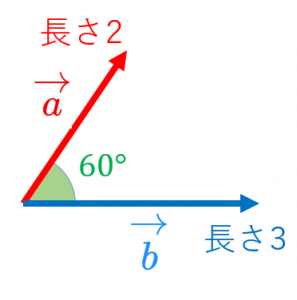
例えば、図において、
$\overrightarrow{a}$ の長さは $2$
$\overrightarrow{b}$ の長さは $3$
なす角は $60^{\circ}$
なので、内積は、
$\overrightarrow{a}\cdot\overrightarrow{b}=2\times 3\times\cos 60^{\circ}=3$
となります。
1.内積と直交
$\overrightarrow{a}$ と $\overrightarrow{b}$ の内積が $0\iff$ $\overrightarrow{a}$ と $\overrightarrow{b}$ は直交
という性質があります。なぜなら、なす角 $\theta$ が $90^{\circ}$ のとき、$\cos\theta=0$ となり、
$\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos\theta=0$
となるからです。
※ $\overrightarrow{a}$ や $\overrightarrow{b}$ の長さが $0$ のときも直交と呼びます。
2.内積と展開公式
$|\overrightarrow{a}-\overrightarrow{b}|^2=|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-2\overrightarrow{a}\cdot\overrightarrow{b}$
という式が成立します。
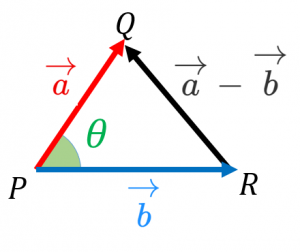
これは、余弦定理:
$QR^2=PQ^2+PR^2-2PQ\cdot PR\cos\theta$
という式をベクトルで表現したものです。
さらに、性質2で $\overrightarrow{b}$ を $-\overrightarrow{b}$ とすることで、
$|\overrightarrow{a}+\overrightarrow{b}|^2=|\overrightarrow{a}|^2+|\overrightarrow{b}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}$
という公式も得られます。
3.成分表示
ベクトルが、$\overrightarrow{a}=(a_1,a_2)$、$\overrightarrow{b}=(b_1,b_2)$ のように成分表示されているとき、
内積は、
$\overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2$
と表すことができます。
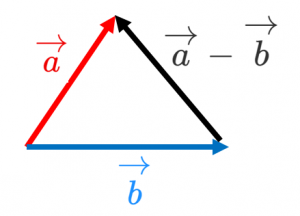
さきほどの公式:
$|\overrightarrow{a}-\overrightarrow{b}|^2=|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-2\overrightarrow{a}\cdot\overrightarrow{b}$
を使うと、
$2\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-|\overrightarrow{a}-\overrightarrow{b}|^2$
となります。
ここで、
$|\overrightarrow{a}|^2=a_1^2+a_2^2$
$|\overrightarrow{b}|^2=b_1^2+b_2^2$
$|\overrightarrow{a}-\overrightarrow{b}|^2=(a_1-b_1)^2+(a_2-b_2)^2$
であることに注意すると、
$2\overrightarrow{a}\cdot\overrightarrow{b}\\
=a_1^2+a_2^2+b_1^2+b_2^2-(a_1-b_1)^2-(a_2-b_2)^2\\
=2a_1b_1+2a_2b_2$
となります。
次回は ベクトルのなす角度の計算(2次元、3次元)と検算ツール を解説します。
