実数を $n$ 個並べたもの全体の集合にユークリッド距離を定めたものをユークリッド空間と言う。
ユークリッド空間とは
$n$ 次元ユークリッド空間 $\mathbb{R}^n$ とは、
1.実数を $n$ 個並べたもの全体の集合
つまり、
$\mathbb{R}^n=\{(x_1,x_2,\dots,x_n)\mid x_1,x_2,\dots,x_n\in \mathbb{R}\}$
という集合に対して、
2.ユークリッド距離を定めたもの
つまり、
$(a_1,a_2,\dots,a_n)$ と $(b_1,b_2,\dots,b_n)$ の間の距離を、
$\sqrt{(a_1-b_1)^2+(a_2-b_2)^2+\cdots +(a_n-b_n)^2}$
で定義したものです。
2次元ユークリッド空間
実数を2つ並べたもの $(x_1,x_2)$ 全体の集合 $\mathbb{R}^2$ を考えます。
例えば、$(3,2),(-1,3.14),(\sqrt{2},-e)$ などは全て $\mathbb{R}^2$ の要素です。
そして、
$\mathbb{R}^2$ の2つの要素 $(a_1,a_2)$、$(b_1,b_2)$ の間の距離を、
$\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}$
で定めます。
つまり、$\mathbb{R}^2$ は、いわゆる普通の直交座標平面とみなすことができます。
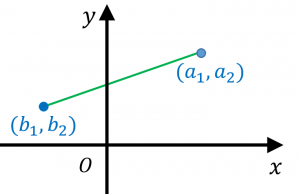
実際、三平方の定理より、緑色の線分の長さは $\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}$ になります。
3次元ユークリッド空間
実数を3つ並べたもの $(x_1,x_2,x_3)$ 全体の集合 $\mathbb{R}^3$ を考えます。
例えば、$(3,2,1),(\sqrt{2},-e,3.14)$ などは全て $\mathbb{R}^3$ の要素です。
そして、
$\mathbb{R}^3$ の2つの要素 $(a_1,a_2,a_3)$、$(b_1,b_2,b_3)$ の間の距離を、
$\sqrt{(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2}$
で定めます。
つまり、$\mathbb{R}^3$ は、高校数学で学ぶ、いわゆる普通の直交座標空間とみなすことができます。
非ユークリッド空間の例
ここまでは、ユークリッド距離という、いわゆる普通の距離を考えてきました。
しかし、実数を $n$ 個並べたもの全体の集合という舞台が同じでも、違う距離を考えれば、ユークリッド空間ではない別の空間となります。
例えば、座標平面の文脈で(平安京や札幌のように)縦と横にしか移動できない状況を考えると、$(a_1,a_2)$ と $(b_1,b_2)$ の間の距離は、ユークリッド距離ではなく、
$|a_1-b_1|+|a_2-b_2|$ という距離を使う方がふさわしいでしょう。
次回は 多変数関数、ベクトル値関数など様々な関数の例 を解説します。
