平均とは、合計÷個数のことです。
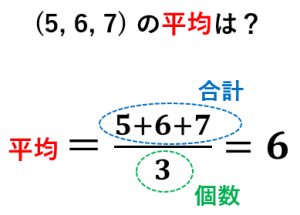
例えば、$(5,6,7)$ というデータだと、合計は $5+6+7=18$ であり、個数は $3$ なので、平均は $18\div 3=6$ です。
※平均のことは平均値、アベレージなどとも言います。
平均の求め方
問題
$5$ 人の体重がそれぞれ $51$kg、$59$kg、$45$kg、$70$kg、$55$kg のとき、平均体重はいくらか?
答え
合計体重は、$51+59+45+70+55=280$kg です。
データの個数(人数)は、$5$ です。
平均は合計÷個数なので、$280\div 5=56$kg となります。
平均値の意味(意義)
例えば、先ほどの体重の問題設定において
「5人の体重はだいたいどれくらい?個々の体重は分からなくてもいいから一言(数字一つ)で表して」
と言われたときの答え(の一つが)平均値(この場合は $56$kg)です。
このように、たくさんの数字を一つの数字で端的に表したいという場面で登場するのが平均です。
注:平均ではなく他の代表値(中央値、最頻値)を用いることもありますが、平均が一番有名です。→中央値の意味と求め方、偶数の場合
式で書いてみる
$n$ 個のデータ $x_1,x_2,\cdots,x_n$ に対する平均は、合計÷個数なので、$\dfrac{x_1+x_2+\cdots +x_n}{n}$
となります。
平均を表す記号としては、上にバーをつけた $\overline{X}$ や、アルファベットの $m$、ギリシャ文字のミュー:$\mu$ が使われることが多いです。
平均の欠点(異常値、外れ値)
例えばさっきの体重の例で、もう一人体重 $200$kg の人を考えてみましょう。$6$ 人の平均体重は、$\dfrac{51+59+45+70+55+200}{6}=80$ となります。
$200$kg の人に引っ張られて平均が大きく上昇してしまいました。
実際に体重が重いのは一人だけなのに、一人あたり80kgの大男集団という印象を受けますね。
このように、平均値は外れ値に大きく引っ張られやすいのでそれが嫌な場合は
・あらかじめ外れ値を除去してから平均を計算
・別の代表値(中央値とか)を使う
・代表値で表現することを諦める
などの対策が必要になります。
次回は 中央値の意味と求め方、偶数の場合 を解説します。
