四角形の内角の和について考えます。
内角の和
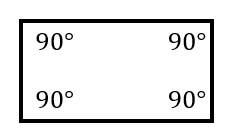
例えば、長方形や正方形は、全ての角度が $90^{\circ}$ であり、全て足すと
$90+90+90+90=360^{\circ}$
になっています。四角形の内角の和がいくつになるのか忘れてしまったら、長方形や正方形を使って思い出しましょう。
この記事の残りでは、四角形の内角の和が360°であることを2通りの方法で証明します。
証明1
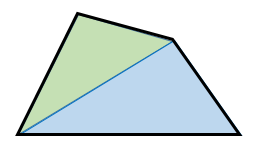
三角形の内角の和が $180^{\circ}$ であるという性質を使います。
すると、
青い三角形の内角の和は $180^{\circ}$
緑の三角形の内角の和も $180^{\circ}$
となります。
よって、四角形の内角の和は、
$180^{\circ}+180^{\circ}=360^{\circ}$
となります。
証明2
四角形 $ABCD$ に対して、
・$A$ を通り $BC$ と平行な直線を引きます。
・$A$ を通り $CD$ と平行な直線を引きます。
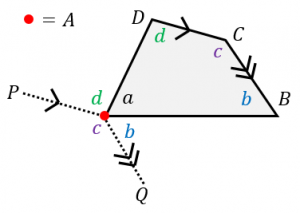
すると、平行線の錯角は等しいので、
$\angle QAB=b$
$\angle DAP=d$
となります。
さらに、$\angle PAQ$ は $\angle DCB$ を平行移動したものなので、大きさは一致し、
$\angle PAQ=\angle c$
となります。
よって、四角形の内角の和は、
$a+b+c+d$
つまり「点 $A$ の周りの一周分の角度」となります。一周分は $360^{\circ}$ なので、四角形の内角の和は $360^{\circ}$ となります。
五角形や六角形だとどうなる?
$n$ 角形の内角の和は $180\times (n-2)^{\circ}$ になります。
例えば、
五角形の内角の和は $180\times 3=540^{\circ}$
六角形の内角の和は $180\times 4=720^{\circ}$
になります。
証明1と同じように、三角形に分けることで証明できます。
次回は 多角形の内角の和の公式を3通りの方法で証明する を解説します。
