方向微分の意味と求め方

方向微分の意味と求め方について、詳しく説明します。

方向微分とは

$f(\overrightarrow{x})$ は入力がベクトルで、出力がスカラーである関数とします。

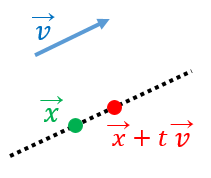
$\overrightarrow{x}$ から、特定の方向 $\overrightarrow{v}$ に微小変化したときの $f$ の変化率は、
$\displaystyle\lim_{t\to 0}\dfrac{f(\overrightarrow{x}+t\overrightarrow{v})-f(\overrightarrow{x})}{t}$
となります。この値を $\overrightarrow{v}$ 方向の方向微分（係数）と言います。
（$\overrightarrow{v}$ として、単位ベクトルのみを考える場合もあります。）

このページでは、方向微分のことを $\nabla_{\overrightarrow{v}}f(\overrightarrow{x})$ と書くことにします。

例題

解答：

方向微分は、
$\displaystyle\lim_{t\to 0}\dfrac{f(1+3t,2+4t)-f(1,2)}{t}\\
=\displaystyle\lim_{t\to 0}\dfrac{(1+3t)^2+(2+4t)^2-1^2-2^2}{t}\\
=\displaystyle\lim_{t\to 0}\dfrac{6t+9t^2+16t+16t^2}{t}\\
=22$
となります。

方向微分を求める公式

$\nabla_{\overrightarrow{v}}f(\overrightarrow{x})=\nabla f(\overrightarrow{x})\cdot\overrightarrow{v}$
という公式が成立します。

例えば、先ほどの例題では、
$\nabla f(x,y)=(2x,2y)=(2,4)$
$\overrightarrow{v}=(3,4)$
であり、これらの内積を計算すると、$6+16=22$ となります。先ほど計算した方向微分と一致しています！

簡単のため、$f$ が二変数関数の場合を考えます。方向を $\overrightarrow{v}=(v_x,v_y)$ とします。このとき、二変数関数のテイラー展開を使うと、
$f(x+tv_x,y+tv_y)\\
=f(x,y)+tv_xf_x(x,y)+tv_yf_y(x,y)+o(t)$
となります。

よって、
$\displaystyle\lim_{t\to 0}\dfrac{f(\overrightarrow{x}+t\overrightarrow{v})-f(\overrightarrow{x})}{t}\\
=\displaystyle\lim_{t\to 0}\dfrac{tv_xf_x(x,y)+tv_yf_y(x,y)+o(t)}{t}\\
=v_xf_x(x,y)+v_yf_y(x,y)\\
=\nabla f(\overrightarrow{x})\cdot\overrightarrow{v}$
となります。

次回は grad、div、rotの定義と意味 を解説します。