ロジット関数:$f(p)=\log\dfrac{p}{1-p}\:(0<p<1)$
ロジスティック関数:$g(x)=\dfrac{A}{1+e^{-k(x-x_0)}}$
統計学(ロジットモデル、ロジスティック回帰分析など)でよく登場する関数です。
ロジット関数のグラフ
確率 $p$ で起こる事象 $A$ について、$A$ が起こる確率と起こらない確率の比 $\dfrac{p}{1-p}$ をオッズと言います。そして、オッズの対数をとったもの $\log\dfrac{p}{1-p}=\log p-\log(1-p)$ を対数オッズと言います。
ここで登場した対数オッズを関数とみなしたもの $f(p)=\log\dfrac{p}{1-p}$ をロジット関数(logit function)と言います。ロジット関数のグラフは下図のようになります。
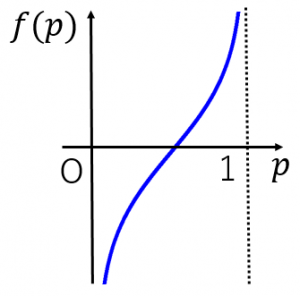
・定義域は $0<p<1$ です。
・$p\to 0$ で $f(p)\to -\infty$、$p\to 1$ で $f(p)\to\infty$ です。
・$p=0$ と $p=1$ が漸近線です。
・$p=\dfrac{1}{2}$ で $f(p)=0$ です。$(\frac{1}{2},0)$ に関して点対称です。
ロジット関数の逆関数
ロジット関数 $y=\log\dfrac{p}{1-p}$ の逆関数を求めてみます。両辺の指数を取ると、
$e^y=\dfrac{p}{1-p}$
$e^y-e^yp=p$
$p=\dfrac{e^y}{e^y+1}=\dfrac{1}{1+e^{-y}}$
つまり、ロジット関数の逆関数は $g(x)=\dfrac{1}{1+e^{-x}}$ です。
これを(標準)ロジスティック関数と言います。
より一般に、標準ロジスティック関数を平行移動、拡大縮小したものも含めて、ロジスティック関数と言います。つまり、
$\dfrac{A}{1+e^{-k(x-x_0)}}$
という形の関数は全部ロジスティック関数と呼びます。
ロジスティック関数のグラフ
標準ロジスティック関数 $g(x)=\dfrac{1}{1+e^{-x}}$ のグラフは図のようになります。
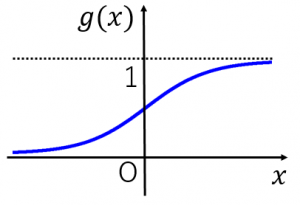
・定義域は実数全体です。
・$x\to \infty$ で $g(x)\to 1$、$x\to -\infty$ で $g(x)\to 0$ です。
・$x=0$ で $g(x)=\dfrac{1}{2}$ です。$(0,\frac{1}{2})$ に関して点対称です。
標準ロジスティック関数はステップ関数をなだらかにしたもの(微分可能)です。シグモイド関数とも呼ばれます。
次回は オッズとオッズ比の意味 を解説します。
