2つの三角形が相似である条件
(i) 2組の角がそれぞれ等しい
(ii) 2組の辺の比とその間の角がそれぞれ等しい
(iii) 3組の辺の比がすべて等しい
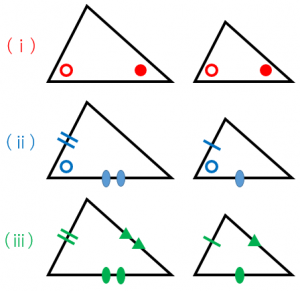
三角形の相似条件を使う例として有名なものを3つ紹介します。
平行線と相似
例題1:図において、$AB$ と $CD$ は平行であるとする。このとき、三角形 $ABX$ と $CDX$ が相似であることを証明せよ。
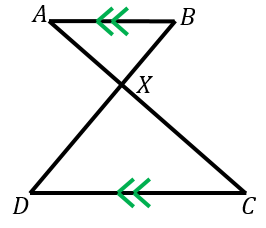
平行線の錯角は等しいので、
$\angle XAB=\angle XCD$
$\angle XBA=\angle XDC$
です。
よって、2組の角がそれぞれ等しいので、条件 (i) より、三角形 $ABX$ と $CDX$ は相似であることが証明できました。
このように、等しい角度はいろいろな図形で登場するので、相似の条件(i),(ii),(iii) の中では (i) を使うことが一番多いです。
「相似を証明せよ」と言われたら、基本的に「等しい角度を2組見つける」と考えましょう。
円周角と相似
例題2:図において三角形 $ABX$ と $CDX$ が相似であることを証明せよ。
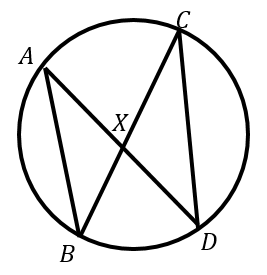
円周角の定理より、
$\angle BAX=\angle DCX$
(どちらも弧 $BD$ に対応する円周角)
$\angle ABX=\angle CDX$
(どちらも弧 $AC$ に対応する円周角)
です。よって、2組の角がそれぞれ等しいので、条件 (i) より、三角形 $ABX$ と $CDX$ は相似であることが証明できました。
中点と相似
例題3:図において、$M$ は $AB$ の中点、$N$ は $AC$ の中点とする。このとき、三角形 $AMN$ と $ABC$ が相似であることを証明せよ。
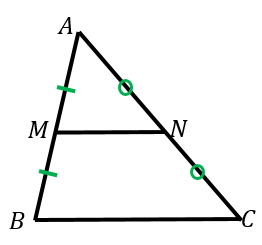
$\angle MAN$ と $\angle BAC$ は同じ角なので、大きさは等しいです。
また、
$AB:AC=2AM:2AN=AM:AN$
となるので、2組の辺の比が等しいことが分かります。
よって、三角形 $AMN$ と $ABC$ は、2組の辺の比とその間の角がそれぞれ等しいので、条件 (ii) より、相似であること証明できました。
ちなみに、例題3は中点連結定理の証明、例題、逆でも登場した有名な図です。
次回は 直角三角形の相似条件 を解説します。
