数学的帰納法の意味と例題２問

数学的帰納法とは

・$n=1$ で命題が成り立つ
・$n=k$ で命題が成り立つなら、$n=k+1$ でも命題が成り立つ
という2つのことが言えるとき、
全ての自然数 $n$ で命題が成り立つ
と言えます。これを使った証明を「数学的帰納法による証明」と言います。

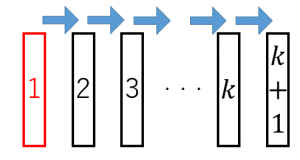
最初の１つが正しくて
一つ右に正しさが伝わるので
全て正しいというドミノ倒しのようなイメージです。

例題１（等式の証明）

$n=1$ のときに正しいことの証明
$1$ から $1$ までの和は $1$
$\dfrac{1}{2}n(n+1)=\dfrac{1}{2}\cdot 1\cdot 2=1$
となり確かに両者は等しいです。

$n=k$ で正しいなら、$n=k+1$ でも正しいことの証明
$n=k$ で正しいなら、
$1+2+3+\cdots + k=\dfrac{1}{2}k(k+1)$
が成立します。

この両辺に $k+1$ を加えると、
$1+2+3+\cdots +k+(k+1)\\
=\dfrac{1}{2}k(k+1)+(k+1)$
となります。

この右辺を $\dfrac{1}{2}(k+1)$ でくくると、
$\dfrac{1}{2}(k+1)(k+2)$
となります。

つまり、$1$ から $(k+1)$ までの和は、$\dfrac{1}{2}(k+1)\{(k+1)+1\}$ となることが分かりました。つまり $n=k+1$ でも主張は正しいです。

以上2つのことから、数学的帰納法により全ての自然数 $n$ に対して $1$ から $n$ までの和が $\dfrac{1}{2}n(n+1)$ と等しいことが証明されました。

例題２（不等式の証明）

$n=1$ のときに正しいことの証明
$n=1$ のとき、$1 < 2^1$ は確かに成立します。

$n=k$ で正しいなら、$n=k+1$ でも正しいことの証明
$n=k$ で正しいなら、
$k < 2^k$
という主張が成立します。両辺に $1$ を加えると、
$k+1 < 2^k+1$
となります。

ここで、
$2^k+1 < 2^{k+1}$
という式（＊）を示せれば、上の不等式と合わせると、
$k+1 < 2^{k+1}$
となり、$n=k+1$ でも $n < 2^n$ という主張は正しいと言えます。

実際、式（＊）の両辺の差は、
$2^{k+1}-2^k-1\\
=2^k(2-1)-1\\
=2^k-1 > 0$
となり（＊）は成立します。

以上2つのことから、数学的帰納法により全ての自然数 $n$ に対して $n < 2^n$ という不等式が成立することが証明されました。

次回は 有効数字の意味と足し算やかけ算の計算 を解説します。