三角形の各辺に接している円(内接円)の半径を、どのように計算するかを説明します。
入試や定期テストでよく出るテーマで、公式を覚えておくと計算が非常に楽になります。
直角三角形の場合
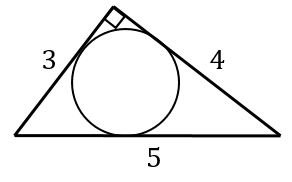
三角形の面積は
\(3 \times 4 \div 2 = 6\)
です。

内接円の中心から各辺に下ろした垂線はすべて長さ \(r\) になります。
よって、三角形を 3 つの小さな直角三角形に分けて考えると、それぞれの面積は
– 赤い三角形:\(\dfrac{3}{2}r\)
– 青い三角形:\(\dfrac{5}{2}r\)
– 緑の三角形:\(2r\)
となります。
3つの面積の和が元の三角形の面積に等しいので、
\(\dfrac{3}{2}r + \dfrac{5}{2}r + 2r = 6\)
整理すると
\(\left(\dfrac{3}{2} + \dfrac{5}{2} + 2\right) r = 6\)
よって
\(6r = 6\)
つまり \(r = 1\) です。
内接円の半径を求める一般公式
上の例題と同じ考え方で、三角形の面積 $S$ と三辺 $a, b, c$ が分かれば、内接円の半径が求められることを示します。
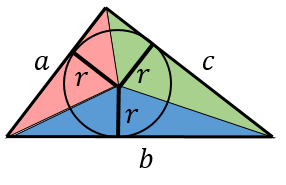
三辺を \(a, b, c\)、内接円の半径を \(r\) とすると、先ほどと同様に
– 赤い部分:\(\dfrac{a}{2}r\)
– 青い部分:\(\dfrac{b}{2}r\)
– 緑の部分:\(\dfrac{c}{2}r\)
となります。
これらの和が三角形の面積 \(S\) に等しいので、
\(\dfrac{a}{2}r + \dfrac{b}{2}r + \dfrac{c}{2}r = S\)
まとめると
\((a + b + c)\dfrac{r}{2} = S\)
よって公式は
\(r = \dfrac{2S}{a + b + c}\)
となります。
公式を使って計算してみよう
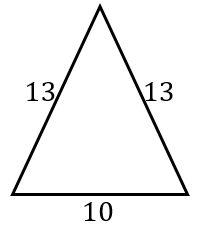
公式
\(r = \dfrac{2S}{a + b + c}\)
を使うため、まず面積 \(S\) を求めます。
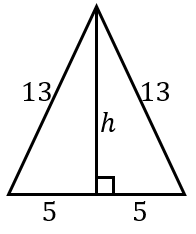
高さを \(h\) とすると、三平方の定理より、
\(h^2 + 5^2 = 13^2\)
\(h^2 = 169 – 25 = 144\)
\(h = 12\)
よって
\(S = 10 \times 12 \div 2 = 60\)
あとは公式に代入するだけです。
\(r = \dfrac{2 \times 60}{13 + 10 + 13}\)
\(= \dfrac{120}{36} = \dfrac{10}{3}\)
二等辺三角形でなくても公式は使えますが、面積計算にヘロンの公式が必要になる場合もあり、少し手間がかかります。
次回は 三角形の重心の定義といろいろな求め方 を解説します。
