| 面の数 | 辺の数 | 頂点の数 | |
| 正四面体 | 4 | 6 | 4 |
| 正六面体 | 6 | 12 | 8 |
| 正八面体 | 8 | 12 | 6 |
| 正十二面体 | 12 | 30 | 20 |
| 正二十面体 | 20 | 30 | 12 |
この表を全て覚えてもよいですが、求め方を覚える方が楽です。
辺の数の覚え方(求め方)
正四面体の各面は正三角形なので、辺の数はのべ $4\times 3=12$ 本です。しかし、$1$ つの辺は $2$ つの面に接しているので、二重に数えられています(図の青と緑)。
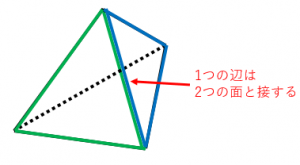
よって、正四面体の辺の数は、$4\times 3\div 2=6$ と計算できます。
面の数×1つの面に含まれる辺の数÷2
で計算できます。
正六面体(立方体)は、$6\times 4\div 2=12$
正八面体は、$8\times 3\div 2=12$
正十二面体は、$12\times 5\div 2=30$
正二十面体は、$20\times 3\div 2=30$
のように計算できます。
頂点の数の求め方その1
正四面体の各面は正三角形なので、頂点の数はのべ $4\times 3=12$ 個です。しかし、$1$ つの頂点は $3$ つの面が集まっているので、三重に数えられています。
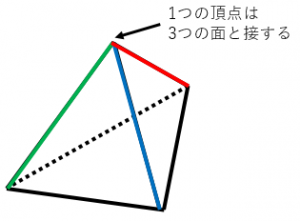
よって、正四面体の辺の数は、$4\times 3\div 3=4$ と計算できます。
面の数×1つの面に含まれる辺の数÷1つの頂点を共有する面の数
で計算できます。
正六面体(立方体)は、$6\times 4\div 3=8$
正八面体は、$8\times 3\div 4=6$
正十二面体は、$12\times 5\div 3=20$
正二十面体は、$20\times 3\div 5=12$
のように計算できます。
頂点の数の求め方その2
実は、どんな多面体でも頂点の数は
辺の数 $-$ 面の数 $+\:2$
で計算することができます。(オイラーの定理)
これを認めてしまえば、簡単に計算できます。
正四面体は、$6-4+2=4$
正六面体は、$12-6+2=8$
正八面体は、$12-8+2=6$
正十二面体は、$30-12+2=20$
正二十面体は、$30-20+2=12$
のように計算できます。
余談
| 面の数 | 辺の数 | 頂点の数 | |
| 正四面体 | 4 | 6 | 4 |
| 正六面体 | 6 | 12 | 8 |
| 正八面体 | 8 | 12 | 6 |
| 正十二面体 | 12 | 30 | 20 |
| 正二十面体 | 20 | 30 | 12 |
・正六面体と正八面体は、
辺の数が同じ、面の数と頂点の数が互いに逆
・正十二面体と正二十面体は、
辺の数が同じ、面の数と頂点の数が互いに逆
次回は 正四面体の展開図2種類の書き方と組み立て方 を解説します。
