正八面体の展開図は全部で11種類
6つの三角形が横に並ぶタイプ:6種類
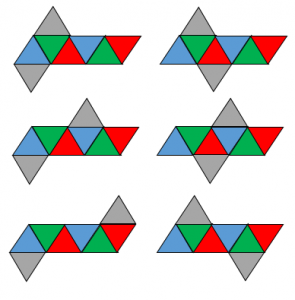
・6つの三角形が横に並ぶ展開図は全部で6種類あります。
青、緑、赤の正三角形6枚が直線に並びます。上側と下側の灰色をそれぞれ青、緑、赤のどれとくっつけるかで $3\times 3=9$ 通りあるように見えますが、回転させて一致するものを除くと6種類になります。
・同じ色で塗られた2つの面は、組み立てたときに互いに平行な面になります。
4つ以上横に並んだとき、3つ隣の三角形は自分と平行な面になります。実際に模型を作って組み立ててみると理解が深まります。
5つの三角形が横に並ぶタイプ:3種類
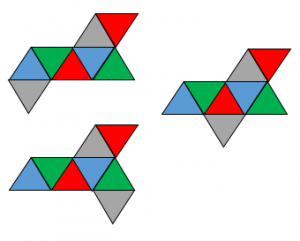
・5つの三角形が横に並ぶ展開図は全部で3種類あります。
3つの展開図は似ています。一番下の灰色の位置が少し違うだけです。
このように、展開図を書く際には「一番長い横のつらなり」を基準にして考えると書きやすい&見やすいです。正八面体の展開図に関する問題を解くときにも「一番長い横のつらなり」を意識しましょう。
4つの三角形が横に並ぶタイプ:2種類
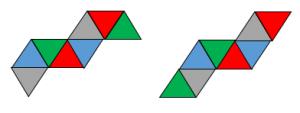
・4つの三角形が横に並ぶ展開図は全部で2種類あります。
この2つも似ています。緑色の正三角形が右上に来るか左下に来るかが違うだけです。
また、4つ以上三角形が横にならばないような展開図はありません。
よって、正八面体の展開図は全部で $6+3+2=11$ 種類です。
対応する辺
それぞれの展開図について、対応する辺(組み立てるときに重なる辺)に同じ番号をつけてみました。
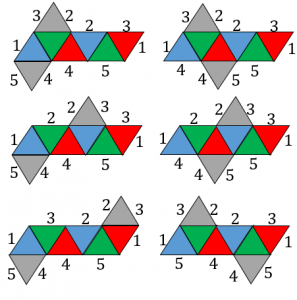
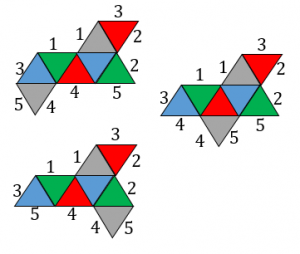
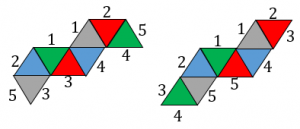
・どの展開図も5つのペアができます。つまり、展開図を組み立てるときには5箇所接着する必要があります。1番から順番にくっつけて組み立てていくのを頭の中でイメージできたら完璧です!
・同じ色の三角形の辺には同じ番号は割り振られません。例えば「1番が両方赤色の三角形の辺」ということはありません。
次回は 確率の意味と簡単な計算の例 を解説します。
