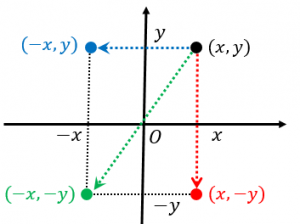
$x$ 軸に関して対称移動:$y$ を $-y$ に変える
$y$ 軸に関して対称移動:$x$ を $-x$ に変える
原点に関して対称移動:$x$ を $-x$ に、$y$ を $-y$ に変える
二次関数の問題を例として、対称移動について説明していきます。
x 軸に関する対称移動
例題1
二次関数 $y=x^2-6x+10$ のグラフを $x$ 軸に関して対称移動させたものの式を求めよ。
解答
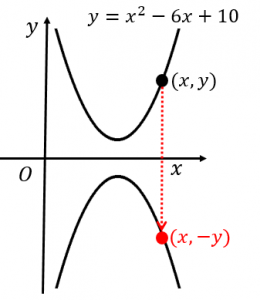
点 $(x,y)$ を $x$ 軸に関して対称移動させると点 $(x,-y)$ になります。
よって、二次関数を $x$ 軸に関して対称移動するには、もとの二次関数の式で $y\to -y$ とすればよいので、
$(-y)=x^2-6x+10$
最後に $y=$ の形に整理すると、答えは
$y=-x^2+6x-10$
となります。
y 軸に関する対称移動
例題2
二次関数 $y=x^2-6x+10$ のグラフを $y$ 軸に関して対称移動させたものの式を求めよ。
解答
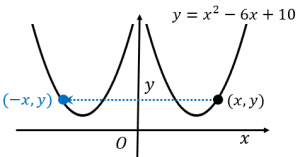
点 $(x,y)$ を $y$ 軸に関して対称移動させると点 $(-x,y)$ になります。
よって、二次関数を $y$ 軸に関して対称移動するには、もとの二次関数の式で $x\to -x$ とすればよいので、
$y=(-x)^2-6(-x)+10$
これを整理すると、答えは
$y=x^2+6x+10$
となります。
原点に関する対称移動
例題3
二次関数 $y=x^2-6x+10$ のグラフを原点に関して対称移動させたものの式を求めよ。
解答
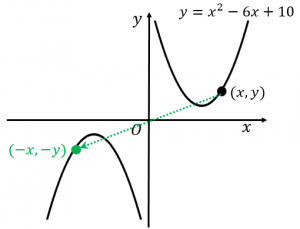
点 $(x,y)$ を原点に関して対称移動させると点 $(-x,-y)$ になります。
よって、二次関数を原点に関して対称移動するには、もとの二次関数の式で $x\to -x$、$y\to -y$ とすればよいので、
$(-y)=(-x)^2-6(-x)+10$
これを整理すると、答えは
$y=-x^2-6x-10$
となります。
補足、まめ知識
・二次関数だけでなく、一般の関数 $y=f(x)$ について、
$x$ 軸に関して対称移動したもの:$y=-f(x)$
$y$ 軸に関して対称移動したもの:$y=f(-x)$
原点に関して対称移動したもの:$y=-f(-x)$
となります。
・「原点に関する対称移動」は「$x$ 軸に関する対称移動」をしたあとで「$y$ 軸に関する対称移動」をしたものと考えることもできます。
次回は ラジアン(rad)の意味と度に変換する方法 を解説します。
