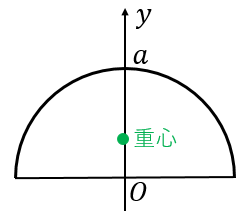
半径 $a$ の半円の重心は、円の中心 $O$ から $\dfrac{4}{3\pi}a$ の位置にある。
半円の重心の求め方について詳しく解説します。
(前半)積分の式を作る
半円の対称軸を $y$ とします。対称性より、半円の重心は $y$ 軸上にあります。中心 $O$ からの距離、つまり重心の $y$ 座標 $y_{G}$ を計算してみましょう。
重心の定義より、$y_{G}=\dfrac{\displaystyle\int y dS}{\displaystyle\int dS}$ となります。$dS$ は微小な図形の面積に対応します。
分母は、半円の面積なので、円の面積公式より
$\pi a^2\cdot\dfrac{1}{2}=\dfrac{1}{2}\pi a^2$
となります。
次は分子です。
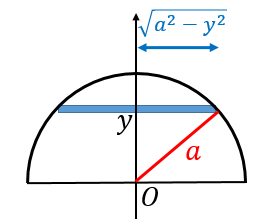
$y$ から $y+dy$ の間にある薄い帯の横の長さは $2\sqrt{a^2-y^2}$ で縦の長さは $dy$ なので、面積はおおよそ $\sqrt{a^2-y^2}dy$ です)。よって、この円板の分子の積分への寄与は $y\cdot 2\sqrt{a^2-y^2}dy$ となります。
これを $y=0$ から $y=a$ まで積分すればよいので、
$y_{G}=\dfrac{\displaystyle\int_{0}^a2y\sqrt{a^2-y^2}dz}{\dfrac{1}{2}\pi a^2}$
となります。
(後半)積分を計算
あとは計算するだけなので簡単です。
$\displaystyle\int_0^a2y\sqrt{a^2-y^2}dy$
は置換積分を使います。
$a^2-y^2=t$ とおくと、$\dfrac{dt}{dy}=-2y$ です。また、$y=0$ のとき $t=a^2$、$y=a$ のとき $t=0$ なので、上式は
$\displaystyle\int_{a^2}^0-\sqrt{t}dt\\
=\displaystyle\int_{0}^{a^2}t^{\frac{1}{2}}dt\\
=\left[\dfrac{2}{3}t^{\frac{3}{2}}\right]_0^{a^2}$
$=\dfrac{2}{3}a^3$
よって、
$y_{G}=\dfrac{\frac{2a^3}{3}}{\frac{1}{2}\pi a^2}$
$=\dfrac{4}{3\pi}a$
補足、まめ知識
・$\dfrac{4}{3\pi}\fallingdotseq 0.42$ です。$0.5$ より少し小さいので「重心は半円の真ん中より少しだけ下の方にありそう」という物理的な直感と一致します。
・重心の座標は長さと同じ次元を持ちます。$y_{G}$ は計算する前から (定数)×$a$ という形になることが分かります。
・半球の重心も似たような考え方で導出できます。立式が少し難しいですが、積分計算はもっと簡単です。
次回は 半球の重心の位置を積分で求める を解説します。
