和集合と積集合の意味と公式

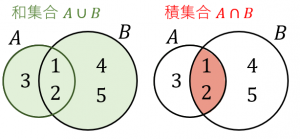
集合 $A$ と $B$ の和集合を $A\cup B$、積集合を $A\cap B$ という記号で表します。

具体例

和集合は、少なくとも片方に入っている要素を集めたものなので、$A\cup B=\{1,2,3,4,5\}$ となります。
積集合は、両方に入っている要素を集めたものなので、$A\cap B=\{1,2\}$ です。

ちなみに、3つ以上の集合に対しても同様です。例えば、さらに集合 $C$ を $C=\{2,6,7\}$ としたとき、
和集合（どれかに入っているもの）は、$A\cup B\cup C=\{1,2,3,4,5,6,7\}$
積集合（全部に入っているもの）は、$A\cap B\cap C=\{2\}$ となります。

他の呼び方、読み方

和集合 $A\cup B$ について
和集合のことを合併、ユニオンと言うこともあります。$A$ または $B$ に入っている要素を集めたものなので、$A\cup B$ のことを「$A$ または $B$」と読むことがあります。

積集合 $A\cap B$ について
積集合のことを共通部分、インターセクション、交叉、などと言うこともあります（特に共通部分はよく使います）。$A$ かつ $B$ に入っている要素を集めたものなので、$A\cap B$ のことを「$A$ かつ $B$」と読むことがあります。

覚え方

「または」の記号 $\cup$ と
「かつ」の記号 $\cap$
を混同しがちなので、覚え方を一つ紹介します。

$\cup$ は上を向いていてコップみたい。雨が降ってきたら水を受け入れる。
→たくさんの要素を受け入れる「または」を表す集合。

$\cap$ は下を向いている。雨が降ってきても水を受け入れない。
→要素をあまり受け入れない「かつ」を表す集合。

和集合と積集合に関連する公式

ドモルガンの法則：
$\overline{A\cup B}=\overline{A}\cap \overline{B}$
$\overline{A\cap B}=\overline{A}\cup \overline{B}$

包除原理（和集合と積集合の要素数に関する公式）：
$|A\cup B|=|A|+|B|-|A\cap B|$
$|A\cup B\cup C|=|A|+|B|+|C|\\
-|A\cap B|-|B\cap C|-|C\cap A|$$+|A\cap B\cap C|$
※ただし、$|A|$ は集合 $A$ の要素数を表します。

次回は 全体集合と補集合の意味と公式 を解説します。