最大公約数:2つの整数に対して、両方ともの約数を公約数と言う。公約数の中で一番大きいものを最大公約数と言う。
具体例
$12$ と $18$ の最大公約数は $6$ です。
実際、$6$ は $12\div 2$ なので $12$ の約数であり、$18\times 3$ なので $18$ の約数でもあります($12$ と $18$ の公約数)。また、$12$ と $18$ の公約数で $6$ より小さいものはありません。
また、$3$ つ以上の数字についても、全てものの約数を公約数と言い、公約数の中で一番大きいものを最大公約数と言います。
例えば $8$ と $12$ と $20$ の最大公約数は、$4$ です(求め方は後述)。
最大公約数の求め方
例題1
$18$ と $24$ の最大公約数を求めよ。
答え1
それぞれの約数を全部書いていって、公約数を探していくのが素直な方法:
$18$ の約数は $1,2,3,6,9,18$
$24$ の約数は $1,2,3,4,6,8,12,24$
最大公約数(=両方ともに登場する最大の数)は、$6$
答え2
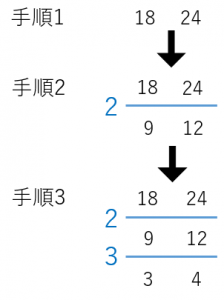
手順1. 最大公約数を求めたい二つの数字を並べる
手順2. 両方ともでわり切れる数を左に書いて、実際にその数でわる(今回は $2$ でわれる)
手順3. 手順2をできるだけ繰り返す(今回は、さらに $3$ でわれる)
手順4. 左に並んだ数字(青い数字)をかけ算すると求めたい最大公約数になる
答えは、$2\times 3=$$6$
3つ以上の場合
数字が3つ以上の場合も、最大公約数の求め方はほとんど同じです。
例題2
$8$ と $12$ と $20$ の最大公倍数を求めよ。
答え1
それぞれの約数を全部書いていく:
$8$ の約数は、$1,2,4,8$
$12$ の約数は、$1,2,3,4,6,12$
$20$ の約数は、$1,2,4,5,10,20$
全部に共通するもの(の中で一番大きいもの)は $4$ である。
答え2
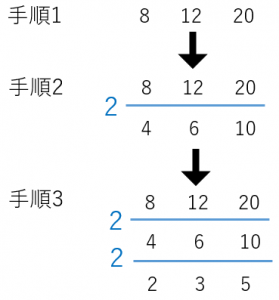
答えは、$2\times 2=$$4$
次回は 平方数(完全平方数)の意味、性質とか を解説します。
